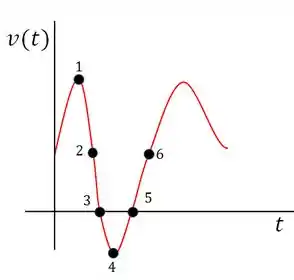
A figura mostra a velocidade de uma partícula que se move em um eixo. O ponto É o ponto mais alto da curva; o ponto é o mais baixo; os pontos e estão na mesma altura. Qual é o sentido do movimento no instante t =0 e no ponto 4 ? Em qual dos seis pontos numerados a partícula inverte o sentido de movimento? Coloque os seis pontos na ordem do módulo da aceleração, começando pelo maior.
Passo 1
O problema pede para dizermos o sentido do movimento de acordo com um gráfico , para isso temos que relacionar a posição com a velocidade, sendo assim vamos olhar a fórmula
Como o tempo é sempre positivo, o sinal da velocidade está diretamente relacionado com o sinal do movimento, nos mostrando assim o sentido da trajetória.
Passo 2
No instante , temos que a velocidade é positiva
Assim,
Por isso podemos afirmar que nesse instante a partícula move-se no sentido positivo do eixo.
Passo 3
Já no ponto temos que a velocidade é negativa (pois o gráfico esta na parte negativa do eixo de velocidade)
Então,
Podemos afirmar assim que a partícula move-se no sentido negativo da trajetória
Passo 4
Como estamos determinando o sentido pelo sinal da velocida se sentido positivo e sentido negativo, temos que no ponto a partícula muda o sentindo do movimento, pois passa de uma velocidade positiva para uma negativa, e no ponto ela passa de uma velocidade negativa para uma positiva.
Passo 5
Para analisarmos a aceleração devemos olhar a tangente de cada ponto, pois aceleração é a derivada da velocidade
Assim o ponto e tem suas retas tangentes horizontais ao eixo , por isso suas acelerações serão zero.
Como estamos analisando os módulos basta ver qual reta está mais inclinada, para obtermos o ponto com maior aceleração, assim vemos que os pontos e tem módulo de aceleração maior que os pontos e
Assim a ordem comenchando do maior das acelerações fica desta forma
Resposta
Sentido positivo
Sentido negativo