O movimento de uma partícula é descrito pelo vetor posição:
Onde e são constantes que valem e .
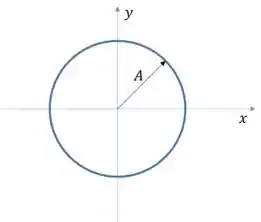
a) Determine o módulo de para qualquer instante de tempo, e desenhe um gráfico da trajetória da partícula, ou seja, o caminho que a partícula faz no plano .
b) Determine o vetor velocidade e a aceleração .
c) Desenhe um gráfico das componentes e da velocidade da partícula como função do tempo.
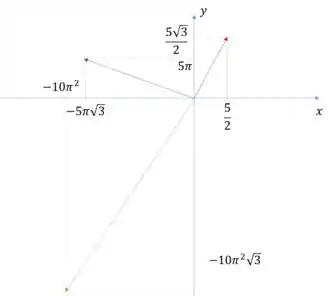
d) Desenhe os vetores posição, velocidade e aceleração para .
Passo 1
a) Como ele quer o modulo do vetor , vamos elevar ao quadrado cada coordenada do vetor dado.
Como sabemos que essa soma e uma constante, podemos tirar da raiz e ver que o modulo não depende das coordenadas.
O que isso significa? Que temos um movimento onde a distância da partícula a origem é constante no tempo, portanto, é um movimento circular!
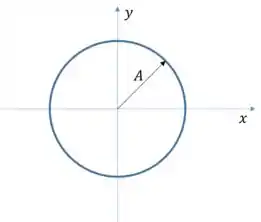
Passo 2
b) Para achar o vetor da velocidade, basta derivarmos em relação ao tempo a expressão do vetor
Passo 3
Para encontrar o vetor da aceleração, basta fazer a mesma coisa, mas agora com o vetor da velocidade:
Passo 4
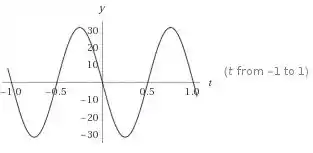
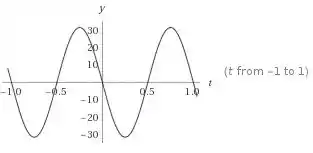
c) Para encontrarmos os gráficos das componentes do vetor velocidade, basta observarmos que uma tem uma função seno e a outra a função cosseno. Então, os gráficos serão bem parecidos com os gráficos das funções seno e cosseno, que já estamos acostumados, que são aquelas “ondinhas”. Aí podemos ir atribuindo alguns valores. Por exemplo, para a componente na direção x:, vamos substituir os valores de e :
Para , temos , pois
Para , temos
Para , temos
E assim, por diante. Aí podemos fazer o gráfico.
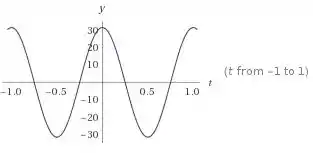
Seguindo o mesmo raciocínio para a componente y, temos:
Passo 5
d) Dado que a velocidade angular é constante, temos que as velocidades nos eixos e constituem uma senoide negativa e uma cossenoide, respectivamente, com amplitude igual a . Logo:
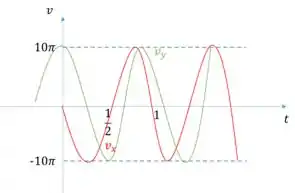
Passo 6
e) Substituindo o valor de e os valores de e :
Esboçando:
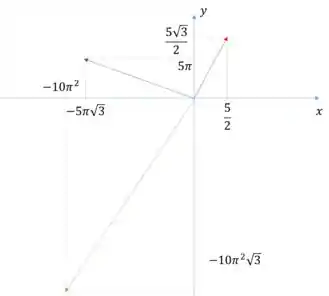
Resposta
a)
b)
c) componente x:
Componente y:
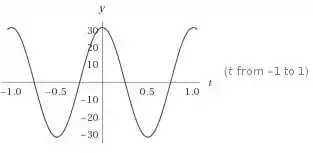
d)
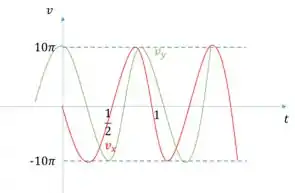
e)