USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 5b
A velocidade de uma partícula é dada por onde está em metros por segundo e em segundos.
b) Determinar a expressão para e fazer os gráficos de e ;
Passo 1
Ooi galerinha do bem,
Nessa questão nos foi dado que a velocidade de uma partícula em função do tempo é dada por:
A partir disso, devemos calcular a aceleração em função do tempo, , e também desenhar os gráficos das curvas e .
Pra determinar a aceleração em função do tempo, como já temos a expressão da velocidade em função do tempo, podemos usar que:
Depois de derivar teremos duas funções representando e . Daí, é só traçarmos o gráfico.
Vamo nessa!
Passo 2
Como vimos, vale que:
Como:
Daí:
Logo:
Ou seja, encontramos uma aceleração constante ao longo do tempo.
Assim, o seu gráfico será uma reta horizontal passando por :
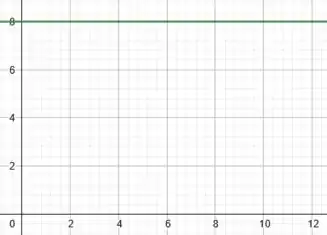
Já para a velocidade, ela é dada pela expressão:
Se colocarmos , vemos que:
Esse é então o coeficiente linear da reta.
O coeficiente angular é justamente o termo que multiplica , ou seja, . Esboçando esse gráfico, vamos ter:
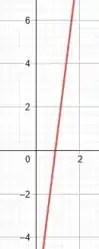
Espero que vocês tenham entendido bem!
Até a próxima 😉