UFSC – Cálculo 1 – Lista 4.1 – Questão 2b
Considere a função f cujo gráfico está representado abaixo. Em cada região marcada, está indicada a medida da área.
- Escreva o resultado das integrais em termos das medidas das áreas
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Bora lá?
O problema nos deu o gráfico de uma função
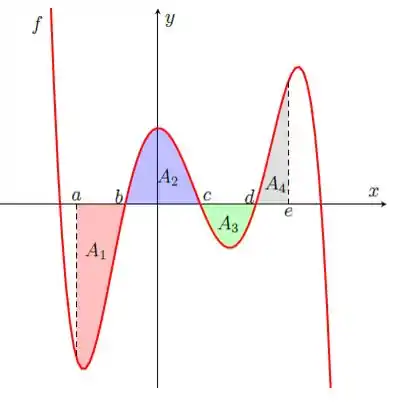
então a ideia aqui é bem tranquila: ir associando cada integral dada com as áreas do gráfico de .
Mas calma, vou fazer passo a passo com você!
Passo 2
As integrais que precisamos calcular são:
vamos começar com a primeira:
Então precisamos verificar qual área está compreendida entre o eixo e a função , entre o intervalo :
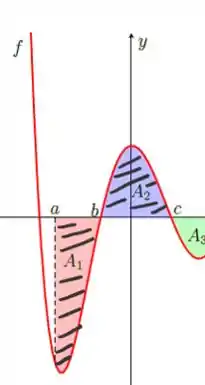
E o resto? O resto não está compreendido nos limites de integração! Então queremos as duas áreas hachuradas e !Atenção na : como ela fica abaixo do eixo o valor da integral é , assim a integral de até é:
Beleza?
Passo 3
Agora vamos ver a região que corresponde a essa integral aqui
Olhando apenas o intervalo teremos três regiões a serem consideradas:
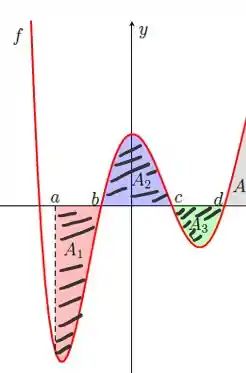
Como as áreas e estão totalmente abaixo do eixo , essas duas são negativas. Já a área está acima do eixo , é positiva:
Tranquilo até aqui?
Passo 4
Agora a integral do intervalo :
No nosso gráfico esse intervalo corresponde à soma de todas as regiões hachuradas:
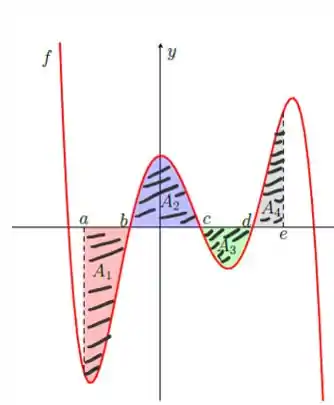
As áreas e estão acima do eixo , então a integral é positiva. Já das outras áreas é negativa. Mas se o limite de integração fosse invertido, o sinal das áreas seria trocado, ok?
Assim essa última área é:
Beleza? E é isso!
Espero ter ajudado! Vamos para a próxima?