UFSC – Cálculo 1 – Lista 4.1 – Questão 1g
Seja A a medida da área da região limitada inferiormente pelo eixo x, superiormente pela função , à esquerda pela reta e à direita pela reta .
(g) Coloque em ordem crescente as respostas dos itens (b) a (f).
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Ela é uma continuação, então vamos recapitular o que sabemos até aqui: fizemos o esboço da região delimitada pelas curvas
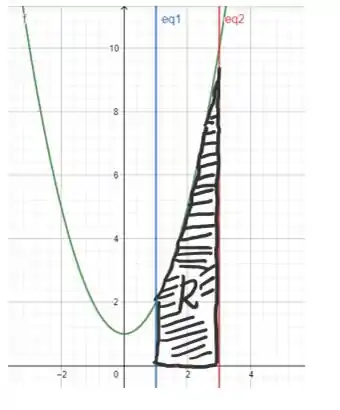
A área é a área correspondente à essa região. E podemos escrever em termos de uma integral:
Esse valor foi obtido integrando a função e aplicando os limites. Esse é o valor exato da área e foi encontrado no item (b).
Nos itens seguintes, o problema pediu para estimar essa região de 4 formas diferentes:
- Pela soma de Riemann pela esquerda e pela direita dividindo em 2 esse intervalo
- E pela soma de Riemann, também pela esquerda e pela direita, mas agora dividindo em 4 partes iguais esse intervalo
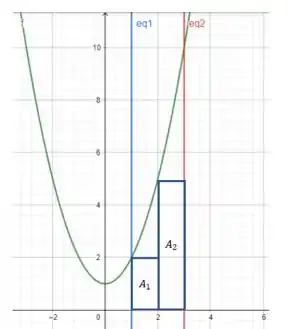
A soma de Riemann pela esquerda é calculada quando usamos o valor da função no ponto mais à esquerda do intervalo como a altura dos retângulos. Quando dividimos a região em 2 (letra (c) do exercício) ficou assim:
E em 4 (letra (e) do exercício) ficou assim:
Note que nesses dois exemplos a estimativa da área é subestimada, pois sobram espaços em branco acima dos retângulos (e abaixo da curva verde) para serem adicionados à área. Por isso dizemos que a soma de Riemann pela esquerda é uma estimativa subestimada.
Nesses dois encontramos os respectivos valores para a área:
Embora a letra (e) chegue mais perto, sendo uma estimativa melhor, ela está aquém do valor real de encontrado quando resolvemos a integral.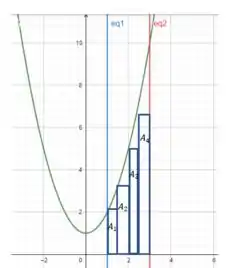
Passo 2
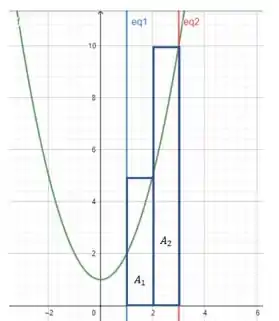Agora vamos ver quando usamos a soma de Riemann pela direita! Agora a altura dos retângulos vai ser o valor da função no extremo direito do intervalo. Quando dividimos o intervalo em 2 (letra (d)) ficou assim:
E quando dividimos em 4 esse intervalo (letra (f) do exercício):
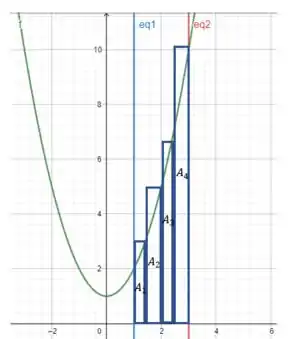
Note que nesses dois casos a área dos retângulos é maior do que a área embaixo da curva, por isso chamamos essa estimativa de superestimada. Os resultados obtidos respectivamente foram:
Quanto maior é o número de retângulos, melhor é a estimativa. Mas como estamos aproximando pela direita, será sempre uma estimativa superestimada
Passo 3
Agora nessa letra o problema nos pede para colocar em ordem crescente os resultados:
- Letra c: Soma de Riemann pela esquerda (2 divisões):
- Letra e: Soma de Riemann pela esquerda (4 divisões):
- Letra b: área exata:
- Letra d: Soma de Riemann pela direita (4 divisões):
- Letra f: Soma de Riemann pela direita (2 divisões):
Assim a ordem correta das letras em ordem crescente é: (c), (e), (b), (d), (f)
Beleza? Espero ter ajudado!
Resposta
(c), (e), (b), (d), (f)