Seja a medida da área da região limitada inferiormente pelo eixo x, superiormente pela função , à esquerda pela reta e à direita pela reta .
(e) Estime o valor de A dividindo o intervalo [1; 3] em quatro partes iguais e usando quatro retângulos abaixo do gráfico de f. Faça um gráfico representando a situação.
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Ela é uma continuação, então vamos recapitular o que sabemos até aqui: fizemos o esboço da região delimitada pelas curvas
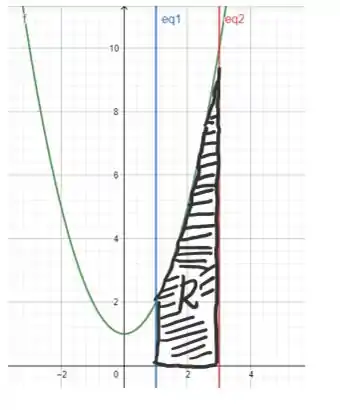

A área é a área correspondente à essa região. E podemos escrever em termos de uma integral:
Agora o problema nos pede para estimar essa mesma região, mas agora utilizando quatro retângulos de bases iguais, dividindo o intervalo em quatro. E mais, pede para calcularmos essa região subestimando a região! Ou seja, abaixo de
Então a ideia aqui é dividir esse intervalo em quatro, achar os retângulos no gráfico da região e estimar somando as áreas desses quatro retângulos!
Mas relaxa, vamos fazer passo a passo juntos!

Passo 2
Vamos começar dividindo o intervalo em !
O intervalo vai de até :
Então temos que o primeiro intervalo é
De até .
O segundo intervalo:
De até ! Vamos para o terceiro intervalo:
Então vai de até . E por fim, o quarto intervalo
Então vai de até .
Tranquilo até aqui?

Passo 3
Agora vamos desenhar dois retângulos com alturas até a função . O primeiro , o segundo , o terceiro e o último :
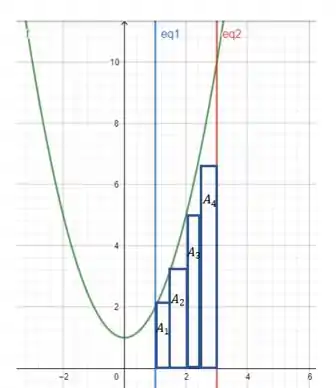
Note que esses com apenas esses quatro retângulos não teremos uma estimativa muito boa para região, mas uma estimativa subestimada
Beleza?
Passo 4
Agora nossa missão é encontrar a área desses dois retângulos aí! A área de um retângulo é


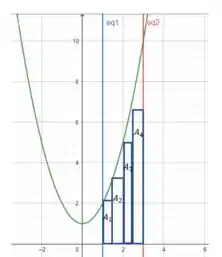
Vamos calcular primeiro (área entre o intervalo ):
Lembrando que , então . Daí a área é:
Beleza? Agora a (área entre o intervalo ):
Mas , aí a área é
Tranquilo até aqui? Agora vamos calcular (área entre o intervalo ):
Mas , aí
E por fim (área entre o intervalo ):
A função em vale e a área do último retângulo é

Por fim a soma das áreas:
Beleza? E é isso! Isso é estimar a área pela soma de Riemann pela esquerda! É uma estimativa ‘por baixo’, estamos subestimando o valor dessa região
Tranquilo?
Espero ter ajudado! Vamos para a próxima?