UFSC – Cálculo 1 – Lista 4.1 – Questão 2c
Considere a função cujo gráfico está representado abaixo. Em cada região marcada, está indicada a medida da área.
- Escreva o resultado em termos das integrais
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Bora lá?
O problema nos deu o gráfico de uma função
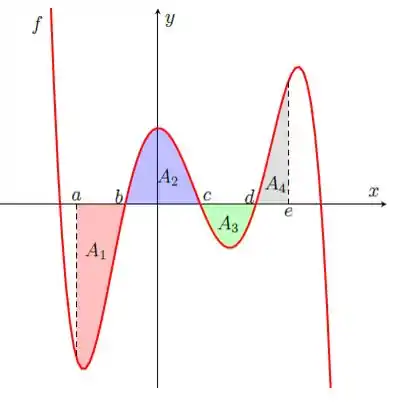
Quando os limites de integração correspondem ao intervalo na ordem crescente, a área correspondente segue o sinal normal: acima do eixo x é positiva, abaixo do eixo x é negativa.
então a ideia aqui é bem tranquila: ir associando cada soma de área dada com as integrais, mas tomando cuidado com os limites de integração!
Mas calma, vou fazer passo a passo com você!
Passo 2
Vamos começar pela primeira soma de áreas:
Analisando o gráfico da função
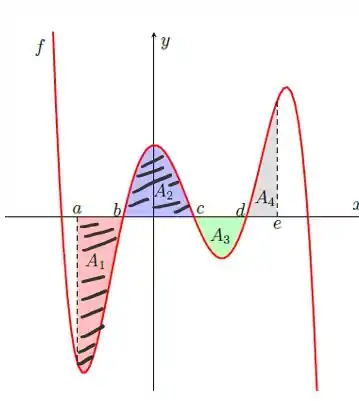
Temos um porém: no intervalo a área é negativa, então para obtermos um resultado positivo na integral, precisamos inverter os limites de integração:
Já para a área não é necessário inverter os limites, pois a área já é positiva. Beleza?
Passo 3
Agora vamos calcular
Olhando para o gráfico, precisamos levar em consideração os intervalos:
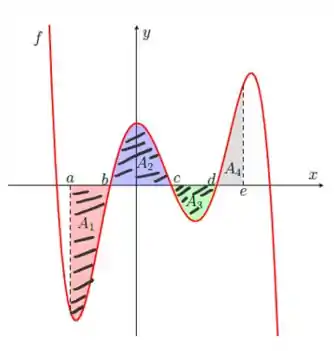
As áreas e são negativas! Então nesses intervalos precisamos inverter os limites de integração:
assim garantimos que o resultado das integrais são todos positivos!
Tranquilo? Vamos para a última soma de áreas?
Passo 4
Precisamos agora somar todas as áreas:
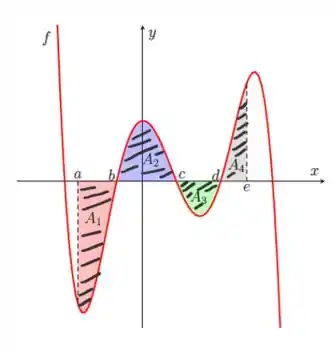Queremos todas as regiões hachuradas:
E aqui de novo: nas integrais que representam as áreas e , para que o resultado seja positivo, precisamos inverter os limites de integração!
Aí a soma de todas as áreas fica assim:
E acabou!
Espero ter ajudado! Vamos para a próxima?