UFSC – Cálculo 1 – Lista 4.1 – Questão 1
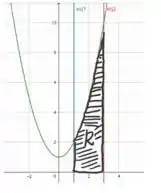
Seja A a medida da área da região limitada inferiormente pelo eixo x, superiormente pela função , à esquerda pela reta e à direita pela reta .
(a) Faça um gráfico representando a situação.
(b) Como A é descrita em termos de integral?
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Bora lá? Vamos começar fazendo um esboço dessa função. A nossa :
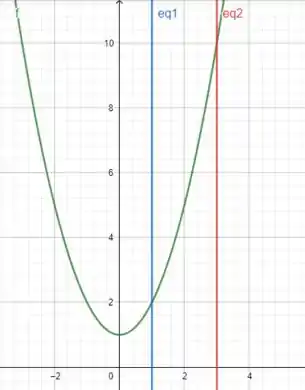
É uma parábola com boca para cima e que corta o eixo (quando ) no . Ela também é limitada pelas curvas (retas verticais) (eq1) e pela (eq2):
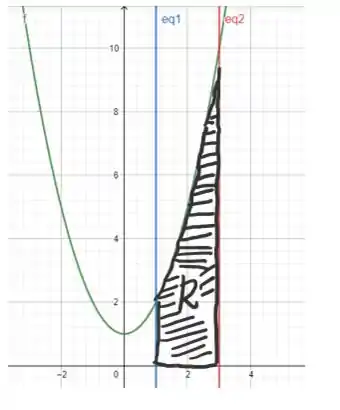
temos assim o esboço da região!
Agora nos resta descrever essa região em termos de uma integral!
Mas calma, vou fazer passo a passo com você!
Vamos lá?
Passo 2
Recapitulando: nossa região R:
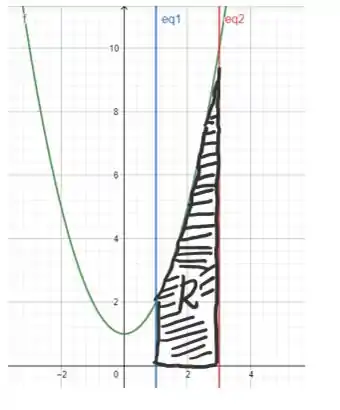
Para representar uma região em termos de integrais precisamos primeiro identificar qual função está ‘por cima’ e qual está ‘por baixo’ em um mesmo intervalo, e isso nós já fizemos!
Digamos que a função por cima seja e a por baixo seja em um intervalo fechado , então a representação dessa região A é
Beleza?
A partir de agora, o problema nos pede para estimar essa área de quatro formas: dividindo o intervalo em dois e estimando pela direita e pela esquerda. E depois dividindo o intervalo em quatro: também pela direita e pela esquerda. Vamos obter resultados menores (os pela esquerda) e maiores (pela direita) que a área exata .
Quanto maior for o número de divisões do intervalo, mais preciso será. Como a integral divide em infinitos pedaços, encontramos o valor exato da área
Beleza?
Mas calma, vou fazer com você os próximos itens!
Espero ter ajudado! Vamos para a próxima?
Resposta
