Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial no R²

Ver Teoria
Exercício 451234567891011121314151617181920212223242526272829303132333435363738394041424344

Enunciado

UFMG – Cálculo 3 – P2 – 2022/2

2) Seja F : R 2 - 0,0 → R 2 o campo dado por:

F x , y = x x 2 + y 2 5 , y x 2 + y 2 5 .

Calcule ∫ γ F ⋅ n   d s , onde γ = x , y ∈ R 2 ; x 2 + y 2 = 1 ,   y ≥ 0 e n é o vetor unitário apontando para fora de γ .

Passo 1

E aii... tudo belezinha??

Nessa questão vamos calcular a integral de linha, que é do caso vetorial.

Daí vamos usar a fórmula:

∫ γ F ⋅ n   d s = ∫ F r t ⋅ n r t r ' t d t  

Onde r t é uma parametrização que vamos achar pra γ .

E:

n r t = 1 r ' t y ' t , - x ' t  

Passo 2

Primeiro vamos esboçar γ pra ver se rola alguma ideia de parametrização:

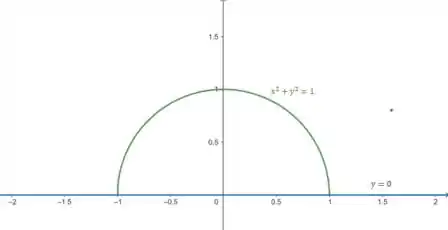
Ohhh.. é uma circunferência de raio 1. Maaas somente a parte positiva de y , porque ele diz que y ≥ 0 .

Quando temos circunferência, uma boa opção pra parametrização é:

x = r cos ⁡ θ

y = r sen ⁡ θ

Como o raio é igual a 1:

x = c o s θ

y = s e n θ

E como só é a metade de cima da circunferência, então podemos dizer que o ângulo θ varia de 0 a π .

Então a equação paramétrica:

r θ = cos ⁡ θ , sen ⁡ θ

E já calculando a derivada:

r ' θ = - sen ⁡ θ , cos ⁡ θ

E o módulo:

r ' t = - sen ⁡ θ 2 + cos ⁡ θ 2

r ' t = 1

Para o vetor unitário:

n r t = 1 r ' t y ' t , - x ' t j ^

n r t = 1 1 cos ⁡ θ , sen ⁡ θ

n r t = cos ⁡ θ , sen ⁡ θ

Passo 3

Jogando lá na fórmula:

∫ γ F ⋅ n   d s = ∫ F r t ⋅ n r t r ' t d t  

= ∫ 0 π cos ⁡ θ cos 2 ⁡ θ + sen 2 ⁡ θ 5 , sen ⁡ θ cos 2 ⁡ θ + sen 2 ⁡ θ 5 ⋅ cos ⁡ θ , sen ⁡ θ 1   d θ

∫ 0 π cos ⁡ θ 1 5 , sen ⁡ θ 1 5 ⋅ cos ⁡ θ , sen ⁡ θ   d θ

= ∫ 0 π cos 2 ⁡ θ + sen 2 ⁡ θ d θ

= ∫ 0 π 1 d θ

= θ 0 π

= π

Acabamos mais uma, heim!? Bora pra próxima...

Resposta

π

Exercícios de Livros Relacionados

Determine o trabalho realizado pelo campo de força F x ,y = xs e nyi + yj em uma partícula que se move sobre a parábola y = x 2 de - 1 ,1 a 2 ,4 .
Seja F x , y = - yi + xj x 2 + y 2 Mostre que ∂ P / ∂ y = ∂ Q / ∂ x .Mostre que ∫ C F ⋅ d r não é independente do caminho. [Sugestão: calcule ∫ C 1 F ⋅ d r e ∫ C 2 F ⋅ d r onde C 1 e C 2 são as metade
Mostre que um campo de força constante realiza trabalho nulo sobre uma partícula que dá uma única volta completa uniformemente na circunferência x 2 + y 2 = 1 .Isso também é verdadeiro para um campo d
Determine uma função f tal que F → = ∇ f e Use a parte (a) para calcular ∫ C F → ⋅ d r → sobre a curva C dada. F → x , y = 3 + 2 x y 2 i → + 2 x 2 y j → , C é o arco da hipérbole y = 1 x de ( 1,1 ) a
Mostre que a integral de linha é independente e calcule a integral. ∫ C 2 x s e nyd x + ( x 2 cos ⁡ y - 3 y 2 ) d y C é qualquer caminho de ( - 1,0 ) a ( 5,1 )