PUCRIO – Cálculo 3 – MAT1163 – 2020.2 – G2 – Parte 1
Considere os vértices , , conforme figura abaixo.
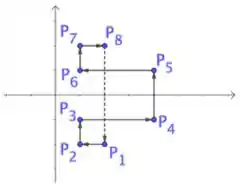
FIGURE . Linhas poligonais com vértices . No item , o lado tracejado não está incluído na linha poligonal. No item , todos os lados estão na linha poligonal.
Considere também o campo vetorial
Para a linha poligonal aberta de vértices percorridos no sentido indicado na figura, calcule
Para a linha poligonal fechada de vértices percorridos no sentido indicado na figura, calcule
Passo 1
Vem comigo arrasar com essa questão!
Para calcularmos as integrais de linha temos que parametrizar as curvas e só que é mais vantagem parametrizar cada segmento dessas curvas e depois integrar um por um utilizando .
A integral geral fica seguinte forma:
Onde e , e são derivadas da parametrização dos seguimentos.
Como estamos mexendo com retas a parametrização vai consistir bem dizer de um dos termos variando em um intervalo e o outro constante.
Passo 2
Vamos primeiro parametrizar cada seguimento de , temos:
portanto e
portanto e
portanto e
portanto e
portanto e
portanto e
portanto e
Então a integral fica da seguinte forma:
Passo 3
Agora vamos resolver essas integrais, temos:
Então temos que:
Passo 4
Agora vamos parametrizar . A parametrização de é igual a do só que mais o seguimento , que é dada por:
portanto e
Então a integral fica da seguinte forma:
Passo 5
Agora vamos resolver essas integrais, temos:
Então temos que:
Com isso finalizamos a questão com sucesso!