Considere a curva
Definida para , e a função escalar
Definida sobre o traço de .
- Esboce o traço de e calcule
- Exprima o comprimento de como uma integral definida (não precisa resolver a integral, mas simplifique)
- Se o traço de for interpretado como um fio e for interpretado como a densidade linear de carga elétrica no ponto desse fio, qual é a interpretação correspondente para
- Existe um campo vetorial tal que ?
Passo 1
Temos a curva , onde
Para obter o traço ou trajetória dessa curva, vamos encontrar a equação cartesiana dela.
Isolando o parâmetro em , temos:
Substituindo em :
Essa é a equação cartesiana da nossa curva então.
Passo 2
Essa equação cartesiana é a equação de uma parábola com concavidade voltada para cima.
Pronto, então pra esboçar o traço dessa curva é só esboçar essa parábola.
CALMA! É quase isso, mas temos que tomar um cuidado especial. Isso porque a nossa curva não está definida para todo e qualquer , mas só no intervalo . Assim, o seu traço se limita a porção dessa parábola entre os pontos e .
Vamos calcular esses pontos então:
Passo 3
Pronto, agora sim podemos esboçar nosso traço:
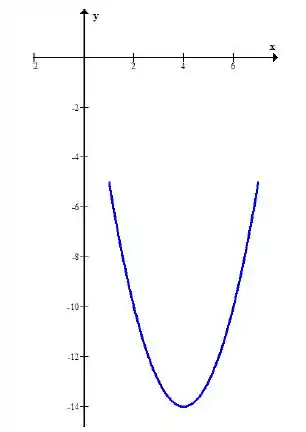
Passo 4
Antes de partir para a letra , a gente ainda tem que calcular .
Pra calcular essa integral de linha, temos que encontrar esse termo , lembra como ele é?
Derivando a parametrização aqui
O módulo disso é
Bem chatinha essa raiz né, mas infelizmente é isso mesmo. Vamos continuar!
Precisamos ver como é a função com os parâmetros de também, olha só
Onde e , com isso
Passo 5
Pronto, vamos colocar tudo na integral agora e calcular!
Pra resolver isso, olha essa substituição que podemos fazer
Olha só, os intervalos são iguais! A integral fica
Passo 6
Vamos exprimir o comprimento da nossa curva agora.
Temos
Conforme vimos no passo anterior.
Assim, a integral que expressa o comprimento da curva é
Passo 7
Integrar a densidade de carga em cada mínimo intervalo da curva, ou seja, em cada nada mais é do que fazer um somatório de todas as cargas “infinitesimais”.
Oi? Como assim?
Pensa o seguinte, quando temos a densidade linear de um fio, o que ela representa?
Ela é “quantidade de massa” por “espaço”, ou seja, g/cm por exemplo. Se somarmos todos esses pequenos intervalos temos a massa total!
Aplicando isso pra densidade de carga linear é praticamente a mesma coisa! Integrar a densidade de carga nos dá como resultado a carga total sobre a curva!
Passo 8
Essa pergunta aí é meio teórica demais, galera. De novo tem que ganhar o ponto do professor na escrita mesmo, não tem conta.
A questão aqui pede pra dizer se existe um campo cuja integral de linha seja igual à , assim
Qual a diferença nisso aí? Bom, na verdade a primeira integral é uma integral de linha caso vetorial, ou seja, . Enquanto a segunda é uma função escalar mesmo.
A resposta depende de um conceito que diz que o campo que resulta na igualdade dessas integrais sempre existe quando a curva é lisa e simples. Em outras palavras, quando a curva é contínua!
Pra provar isso é só mostrar que a derivada da parametrização existe em todos os pontos do domínio!
No caso , então pra qualquer existe a derivada. Portanto com certeza existe um campo que satisfaça o pedido do enunciado. =D
Resposta
A carga total sobre a curva
Sim