Seja .
- Calcule
onde é a curva
Passo 1
- Bom, temos aqui uma questão super direta que já da tudo o que a gente precisa.
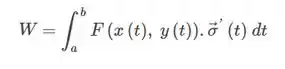
Fazendo as substituições da parametrização que foi dada:
Seja .
onde é a curva
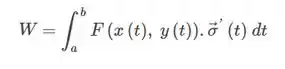
Fazendo as substituições da parametrização que foi dada: