Sejam e a curva com . Então é:
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
Temos que calcular então o trabalho de um campo de forças sobre um caminho.
AAN? Isso mesmo, quando nós temos algo do tipo significa a integral do trabalho, e havendo o caminho, por exemplo a integral do trabalho sobre esse caminho é dado por . assim:
“então ok... Como eu posso resolver isso, Mogli?” Existem diversas maneiras, a mais simples e geral, é pela parametrização da curva, e uma vez parametrizada a curva podemos aplicar ao campo de forças e ver como o campo de forças reage a esse caminho.

Como assim, né? Veja:
Sendo e os limites de integração para . Isso facilita e muito, né?! Bora lá?!
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Temos então que:
E agora nós temos dois trabalhos: derivar a curva e aplicá-la ao campo de forças. Qual quer fazer primeiro? Eu costumo derivar, mas você pode fazer como quiser 😊
Assim:
Aplicando em
E ponto, temos tudo já que precisamos!
Passo 3
Assim:
Aplicando o produto interno:
Sabendo que a integral da soma é a soma das integrais, podemos fazer:
E agora podemos fazer as integrais uma a uma.
Passo 4
Para
Aqui é necessária uma malandragem da nossa, parte. Como assim? Essa é uma função extremamente complicada de complicada, e bom, para uma prova de 2h um professor – pelos menos ajuizado hahaha- não faria isso. Então há alguma técnica por detrás que facilite isso,
Bom, sabemos que a integral simétrica de uma função ímpar é nula. Como assim? Se nós temos uma função ímpar () em um intervalo simétrico ( até 1, até ), então essa integral é nula. Como sei disso? Veja o seno, por exemplo, bom, o seno é uma função ímpar, e vamos ver seu intervalo?
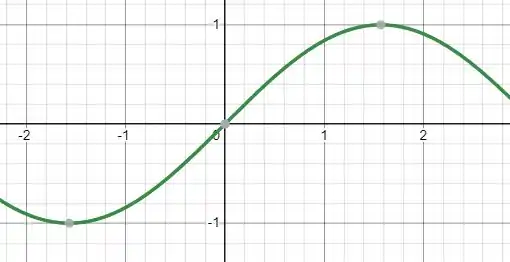
Veja que tudo que está de um lado está o oposto do outro, de forma que eles se cancelam.
Agora sabendo disso, vamos ver se nossa função é ímpar?
Se fizermos :
VEJA, ELA É ÍMPAR E EM UM INTERVALO SIMÉTRICO, LOGO ELA É NULA!! Por essa o seu professor não esperava né hehuehe
Para
Integrando em :
Para
Integrando em :
Para
Usamos o argumento de que uma função impar em um intervalo simétrico se cancela, mas e uma função par em um intervalo simétrico?! Ora bolas, ela se soma. Como é uma função par? , e a nossa função é par? Vamos ver:
Se fizemos :
Mas , assim:
E concluímos que nossa função é par! Assim:
Pegando somente o valor absoluto
Integrando em :
E feito tudo vamos juntar os valores da integral novamente.
Passo 5
Achamos então o nosso resultado:
Que alternativa é essa? A alternativa d)
E acabamos por aqui, carinha! Obrigado por ter vindo até aqui junto comigo 😊
Resposta
Letra d)