Considere as funções
- Encontre
- Usando (a), encontre e determine o seu domínio ;
- Determine o conjunto C onde podemos aplicar a regra da cadeia para calcular ;
- Usando a Regra da Cadeia, encontre
- Compare (b) e (d);
- Esboce os gráficos de e ;
- Indique nos gráficos os pontos onde e não são diferenciáveis.
Passo 1
Temos que armar a composta de em
Reparem, os pontos onde as funções mudam seus domínios são , para , e , para . Nesse caso, devemos dividir a função composta em três regiões: uma para , outra para e a última para .
Assim, colocamos, em cada um dos três intervalos, uma função dentro da outra:
Antes de , temos e valendo . Assim
Entre e , temos e . Como é constante nessa região, também será:
Por fim, na última região, para teremos:
Ou seja, a função vale para valores menores que , e para valores maiores que . No fim das contas, será igual a !
Passo 2
As duas partes da função são contínuas no seu intervalo, resta ver se também são no ponto de mudança, :
Nesse caso, para saber se é derivável, vemos que a função é polinomial em todo seu domínio, de modo que sua derivada para será dada por:
Nesse caso, como é um ponto contínuo de , vemos suas derivadas laterais para determinar sua derivada aí:
Então,
E seu domínio corresponde a todo o conjunto dos reais.
Passo 3
Vimos que e são deriváveis sempre. Então a questão é observar aonde é derivável para observar aonde podemos derivar pela Regra da Cadeia, pois ela dependerá da derivada :
Observando o domínio de , na região onde ela é constante igual a , temos que a função é contínua e derivável, porém o módulo de terá problema na derivada onde ele muda de sinal.
Ou seja, no “bico” desse , em , teremos a derivada inexistindo.
Além disso, resta observar se a função é contínua e derivável no ponto de mudança de domínio, em :
Nesse caso, para saber se é derivável, vemos que a função é polinomial em todo seu domínio, de modo que sua derivada para será dada por:
Então, a derivada lateral de terá problemas em :
Enfim, não será derivável em e .
Dessa forma, o conjunto onde podemos aplicar a regra da cadeia para calcular é:
Passo 4
Pela Regra da Cadeia, nos três intervalos, teremos:
Enfim, obtivemos o mesmo resultado do item , porém nos pontos de mudança achamos que a função não será derivável, em e :
Passo 5
Comparando os intens e , reparamos a diferença na existência da derivada de e no item e a não-existência de ambas no item .
Passo 6
Basta desenhar cada reta ou parábola no seu respectivo domínio, dadas as funções aí explicitadas. Assim, o gráfico ficaria com essa cara:
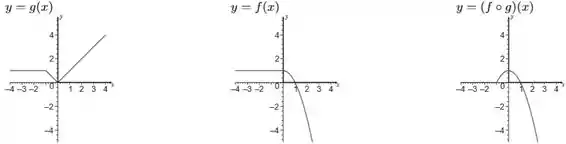
(Extraindo do gabarito oficial)
Passo 7
Analisando os bicos das funções veremos onde não são deriváveis.
Temos bicos em : não é derivável em e .
Não temos bicos em
Temos bicos em : não é derivável em
Resposta
E seu domínio corresponde a todo o conjunto dos reais.