Dizemos que a função f possui derivada lateral à esquerda no ponto x = a quando existe o limite:
De maneira análoga definimos derivada lateral à direita . Mostre que f é derivável no ponto x=a se, e semente se, as derivadas laterais existem e são iguais.
Passo 1
Fala galera, tudo blz? Essa questão quer que provemos o teorema das derivadas laterais. Então, antes de tudo, vamos relembrar o que esse teorema nos diz: “Uma função será derivável em um ponto se existirem derivadas laterais nesse ponto e se essas derivadas laterais forem iguais. ”
Pois bem, para respondermos essa questão podemos pensar em uma função f(x) onde suas derivadas laterais existem, porém, não são iguais. Vamos nessa:
Seja f a função definida por:
Passo 2
Agora, vamos encontrar suas derivadas laterais no ponto a = 3:
- =
=
-
- Em azul a função , ou seja, para valores de ;
- Em vermelho a função , ou seja, para valores de .
Com isso, provamos a existência das derivadas laterais, no entanto elas não coincidiram. O que vai contra uma das condições de existência da derivada.
Passo 3
Agora, vamos ver graficamente o que está acontecendo:
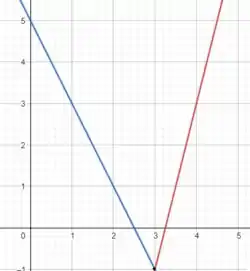
Quando analisamos esse gráfico chegamos a seguinte conclusão, exatamente no ponto , tem-se a formação de uma “ponta” ou “bico”, e podemos ver q nesse ponto podem passar uma infinidade de retas, mas nenhuma dela será tangente ao gráfico, no exatamente pela existência dessa ponta. Então, para que uma função seja derivável em determinado ponto, é necessário que nesse ponto exista uma suavidade no traçado do gráfico, e é o que não acontece nesse exemplo.
Resposta
Feito o estudo das derivadas laterais da função exemplo em questão:
, foi possível observar que como as derivadas laterais não coincidiram, houve a formação de uma “ponta” no gráfico, exatamente no ponto estudado, logo, não existirá nenhuma reta tangente ao ponto, e a reta tangente é exatamente a derivada da função f(x).
∴ se não tem reta tangente no ponto em questão, a derivada da função também não existe.