Diferenciabilidade de uma Função
Use o gráfico da função para determinar os valores de em que a função é diferenciável e indique os valores de em que a derivada é (i) nula (ii) positiva (iii) negativa.
Passo 1
Começamos abrindo essa função em cada uma das suas regiões:
O gráfico de , na região de fica mais ou menos assim:
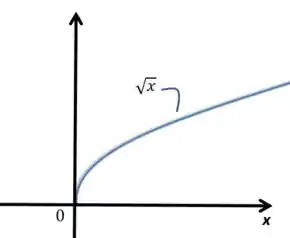
Acontece que onde o gráfico estará sendo aplicado por valores negativos. Com isso, multiplicando com o menos dentro da raiz, esse gráfico acabará sendo o mesmo do , porém espelhado para o outro lado. O gráfico final vai ficar assim:
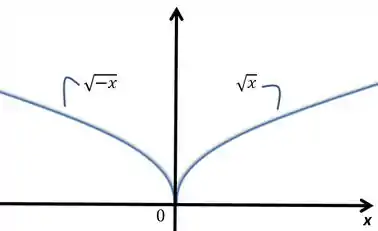
Passo 2
Assim, podemos analisar as derivadas.
A derivada não existe em , pois lá a função tem um “bico”, gerado pelo módulo.
A derivada é negativa para , pois nessa região a função é decrescente.
A derivada é positiva em , pois nessa região a função é crescente.
A derivada não é nula em ponto nenhum, pois fora a função não muda seu crescimento em nenhum outro ponto.