Seja .
Esboce o gráfico de
Dê os pontos onde é duas vezes diferencial e determine e .
Passo 1
Vamos desenhar o gráfico desse módulo de parábola. O processo deve ser desenhar a própria parábola, descobrindo suas raízes e depois “espelhando” toda a região abaixo do eixo para cima.
Descobrindo as raízes da parábola, teremos:
Como essa parábola tem concavidade para cima, a gente sabe que a parte negativa dela está entre suas raízes, e . Com isso, espelhando essa região teremos esse gráfico:
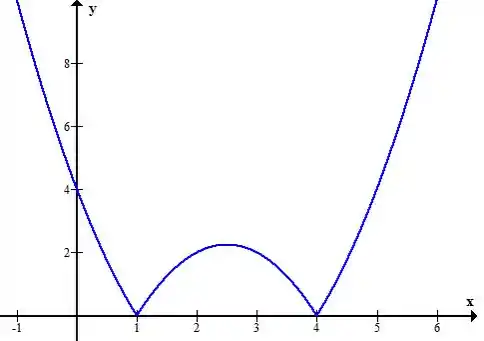
Passo 2
Onde essa função será diferenciável? Repara, o polinômio, quando está fora do módulo, é sempre derivável para quantas vezes quisermos. Quer dizer, se a função fosse só nós saberíamos que ela é derivável sempre, para todos os reais, na derivada primeira, segunda, terceira, ... -ésima derivada.
O problema do módulo é gerar dois “bicos” ali que complicam para a primeira derivada e, portanto, para a segunda derivada, terceira e por aí em diante.
Logo, quais são os únicos pontos em que e não estão definidos?
Logo, é duas vezes diferenciável para todo real menos e : .
Passo 3
Para derivar a função, onde ela pode ser derivável duas vezes, começamos abrindo em forma de módulo:
Derivando esse cara, teremos:
Com isso
Passo 4
O mesmo para a segunda derivada.
Juntando isso em forma de chave, teremos: