Use o gráfico da função para determinar os valores de em que a função é diferenciável e indique os valores de em que a derivada é (i) nula (ii) positiva (iii) negativa.
Passo 1
No intervalo o gráfico será a parábola , cuja concavidade é para baixo e as raízes são (só será usada a, pois a outra não está no intervalo ). Já no intervalo , o gráfico é a parábola , cuja concavidade é para baixo e a raiz que será usada é .
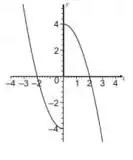
Passo 2
Podemos analisar as derivadas.
A derivada não existe em , pois a função não é contínua nesse ponto, o que pode ser percebido pelo “pulo” que ela dá em . Portanto, é diferenciável em
Passo 3
A derivada é negativa no intervalo , pois nessa região a função é decrescente.
A derivada nunca é positiva, pois a função nunca é crescente.
A derivada não é nula em nenhum ponto.