Derivadas de Ordem Superior
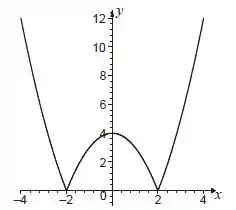
Seja .
- Dê os pontos onde é duas vezes diferencial e determine e
- Esboce o gráfico de
Passo 1
Primeiramente, vamos abrir a função como módulo, ou seja, dizer que ela vale ela mesma quando for maior que zero e que vale seu oposto quando for menor que zero.
Vamos calcular as derivadas dessa função nos dois domínios (em e em ), nos pontos de mudança na lei de formação devemos usar a definição de derivada.
Passo 2
Começando então pelos por esses pontos problemáticos e , vamos calcular os limites laterais:
Opa, esses limites laterais não batem.
Isso significa que o gráfico da nossa função forma um “bico” nesses pontos e, assim, a derivada não existe.
Dessa forma, nossa função é duas vezes diferenciável sempre que e .
Passo 3
Agora, para derivar essa função, como só teremos derivadas fora de e , é só a gente derivar normalmente a função chaveada:
Passo 4
Para fazer a derivada segunda, seguimos a mesma ideia.
Passo 5
Agora vamos desenhar o gráfico da nossa função modular.
Para isso, vamos primeiro imaginar como seria o gráfico dessa função caso ela não fosse modular, isto é, caso tivéssemos
Isso é uma parábola:
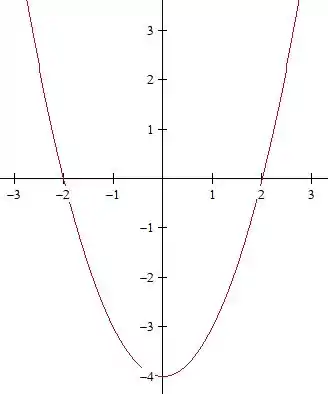
Beleza, agora vamos pensar: o que que o módulo faz com uma função? Qual a ideia do módulo?
O módulo pega os valores negativos de uma função e transforma eles em valores positivos.
Assim, toda essa parte da parábola que está abaixo do eixo (negativa), deve ser “espelhada” para cima.
Fica assim:
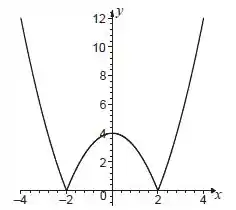
Resposta
- é duas vezes diferenciável para ; e ;
