Use o gráfico da função para determinar os valores de em que a função é diferenciável e indique os valores de em que a derivada é (i) nula (ii) positiva (iii) negativa.
Passo 1
Começamos abrindo essa função em cada uma das suas regiões:
O gráfico de , na região de é uma reta de coeficiente angular . A reta será exatamente igual à reta , só que rebatida em torno do eixo . O gráfico de , portanto, é assim:
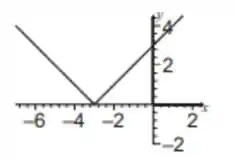
Passo 2
Assim, podemos analisar as derivadas.
A derivada não existe em , pois lá a função tem um “bico”, gerado pelo módulo.
Portanto, a função é diferenciável em
Passo 3
A derivada é negativa para , pois nessa região a função é decrescente.
A derivada é positiva em , pois nessa região a função é crescente.
A derivada não é nula em ponto nenhum, pois não há nenhuma região horizontal no gráfico.