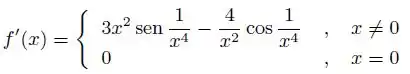Regras de Derivação
Derive a função (se possível, simplifique antes e/ou depois de derivar).
Passo 1
A primeira coisa que temos que fazer é verificar se a função é contínua em . Se ela não for contínua, não vai ser derivável. Depois de verificar se a função é contínua, temos que verificar se as derivadas laterais existem e são iguais.
Para a função ser contínua devemos ter:
Vamos calcular esse limite então.
Passo 2
Vamos dar uma manipulada no nosso limite:
Vamos usar o Teorema do Confronto!
Então:
Assim:
E a função é contínua!
Passo 3
Agora vamos ver as derivadas laterais:
Para nossa função ser derivável, essa derivada que achamos precisa ser zero quando . Contudo, porém, entretanto, todavia, temos x no denominador, então da ruim. Vamos usar o Teorema do Confronto de novo pra calcular essa derivada em :
Para a primeira parcela, temos:
Já para a segunda parcela:
E o limite também da zero.
Então, a função será derivável em ! Teremos nesse ponto.
Resposta
