Uma barra de comprimento e resistência é colocada sobre dois trilhos numa região de campo magnético uniforme cujo módulo é . Os trilhos estão ligados a uma fonte de tensão . Determine a corrente que flui pelo condutor quando:

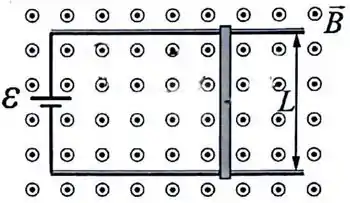
(a) A barra está em repouso

(b) A barra está se movendo para direita com uma velocidade

(c) Em que sentido e com que velocidade devemos mover o condutor para que a corrente através dele seja nula?

(d) Em que sentido e com que velocidade devemos mover o condutor para que o módulo da corrente através dele seja o mesmo módulo da corrente que o atravessava quando ele estava em repouso?

Agora temos que a barra se move! Tomando com a posição horizontal da barra em relação à fonte de forma que a área do circuito fechado seja , temos que o fluxo do campo magnético é dado por

Assim temos que pela lei de Faraday haverá uma força eletromotriz induzida dada por

Pela lei de Lenz, a corrente induzida tem que ser tal que produzirá um campo magnético que tentará frear a variação de fluxo de campo magnético.

Como o fluxo aumenta em módulo com o passar do tempo e o campo magnético externo sai da página temos que o campo magnético produzido pela corrente induzida, tem que entrar na página.

Pela regra da mão direita, para que isso aconteça, a corrente induzida está no sentido horário. Logo vamos defini-la como positiva.

E a corrente induzida é dada por

Assim a corrente total é dada por

Para que a corrente seja nula, basta fazer

Como , temos que mover a barra para a esquerda.

Aqui queremos que a corrente total tenha a mesma intensidade de quando a barra não se movia, ou seja, . Temos duas opções:

-

Nesse caso, temos

Que é o caso da barra parada.

-

Como , temos que mover a barra para a esquerda.