Halliday - Vol. 3 – 9º edição – Capítulo 30 – Seção 4 – Exercício 12
(Capítulo 30.4 – Exercício 12) Na figura 30-39, uma espira retangular de dimensões e é submetida a um campo magnético . Determine (a) o módulo e (b) o sentido (horário ou anti-horário ou “nenhum”, se ) da força eletromotriz induzida na espira se . Determine (c) e (d) o sentido de se Determine (e) e (f) o sentido de se Determine (g) e (h) o sentido de se Determine (i) e (j) o sentido de se
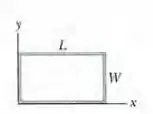
Passo 1
E aeeee pessoal!
Mais uma vez, vamos falar sobre força eletromotriz e a Lei de Faraday!
A expressão para calcular a força eletromotriz é a seguinte:
O sinal negativo mostra que a força eletromotriz se opõe à variação do fluxo.
Então vamos usar isso em cada um dos itens, fechou?
Passo 2
a,b) Aqui temos e queremos calcular o módulo e o sentido da força eletromotriz
Bom, para que seja induzida uma fem, o campo magnético deve ter uma componente perpendicular à espira e deve variar com o tempo. Assim, para a primeira situação temos um campo igual a , que não está variando no tempo. Logo, não temos força eletromotriz e não há nenhum sentido para ela!
Passo 3
A letra (c) já nos dá um campo igual a Esse já apresenta variação do campo ao longo do tempo (olhem ali o ). Vamos calcular a fem!
O que nos dá e o sentido da fem é horário!
Passo 4
A letra (e) nos dá um campo igual a Esse campo apresenta variação, o que implica na existência de uma força eletromotriz!
Assim, a fem induzida é:
O que nos dá e o sentido da fem é anti-horário!
Passo 5
A letra (g) nos dá um campo igual a Isso vai implicar em fluxo magnético igual a zero () e, assim, não há fem induzida e nem sentido.
Passo 6
A letra (i) nos dá um campo igual a Isso vai implicar em fluxo magnético igual a zero () e, assim, não há fem induzida e nem sentido.
Fechouuu
Resposta
- Para , ;
- Nenhum;
- Para
- Horário;
- Para
- Anti-horário;
- Para
- Nenhum;
- Para ;
- Nenhum.