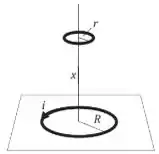
A figura abaixo mostra duas espiras de fio em forma de anel, que tem o mesmo eixo. O anel menor está acima do maior, a uma distância que é grande, comparada com o raio , do anel maior. Em consequência, com a passagem da corrente pelo anel maior (veja figura), o campo magnético correspondente é aproximadamente constante através da área plana , limitada pelo anel menor. Suponha agora que a distância não seja fixa, mas que varie na razão constante
(a) Determinar o fluxo magnético através da área limitada pelo anel menor em função de .
(b) Calcular a f.e.m. gerada no anel menor, no instante em que for igual a .
(c) Determinar o sentido da corrente induzida no anel menor, se .
Passo 1
(a) Determinar o fluxo magnético através da área limitada pelo anel menor em função de .
O módulo do vetor indução magnética promovito por uma corrente em uma espira circular a uma distância do seu centro é dado por:
No entanto, para , teremos que:
Assim, para o fluxo, teremos que:
Passo 2
(b) Calcular a f.e.m. gerada no anel menor, no instante em que for igual a .
A taxa de variação do fluxo é dada por:
Logo, a força eletromotriz será dada por:
Por fim, para , temos que:
Passo 3
(c) Determinar o sentido da corrente induzida no anel menor, se .
Para , temos . Assim, a corrente induzida na espira menor terá o mesmo sentido da corrente da espira maior.
Resposta
(a)
(b)
(c) Mesmo sentido da corrente da espira maior.