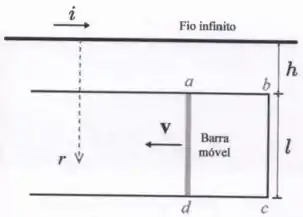
A figura abaixo ilustra um fio retilíneo infinito percorrido por uma corrente elétrica . Uma barra condutora móvel, de comprimento , move-se para a esquerda com velocidade constante entre dois trilhos horizontais. Os trilhos são paralelos entre si e também paralelos ao fio infinito. A extremidade direita dos trilhos é conectada a uma barra condutora vertical fixa, de tal forma que o conjunto (ou seja, os trilhos e a barra fixa) forma uma espira retangular condutora . O trilho superior encontra-se a uma distância do fio infinito.
- Usando a lei de Ampère, calcule o módulo do campo magnético gerado pelo infinito a uma distância arbitrária do mesmo.
- Calcule o módulo da força eletromotriz induzida na espira retangular .
- O sentido da corrente induzida na espira retangular será horário ou anti-horário? Justifique, sucintamente, sua resposta.
Passo 1
a) Neste item, é muito importante relembrar as características de simetria que o fio “infinito” tem, o que nos dará, consequentemente, quais são as características do campo magnético produzido pela corrente .
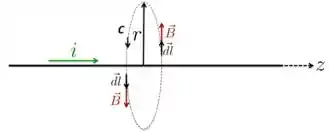
Para entender essas características, vamos sempre ficar de olho na figura abaixo, que mostra o fio envolvido por uma circunferência de raio concêntrica ao fio “infinito”.
Resumão:
- Se girarmos o fio em torno de um eixo que passa longitudinalmente por ele, o fio continua o mesmo. Consequência: o campo magnético tem o mesmo valor em todos os pontos da circunferência de raio concêntrica ao fio;
- Se transladamos o fio ao longo da direção do eixo , o fio também não se altera. Consequência: o campo magnético não tem componente ao longo de , portanto, o campo é perpendicular ao fio e só depende de ;
Portanto, , ou seja, campo depende de e está ao longo da direção tangente ao círculo de raio . Por isso, vamos considerar nossa amperiana (curva fechada da figura) orientada no mesmo sentido e direção de . Isso significa que é paralelo , como colocamos na figura, e a lei de Ampère fica:
em que é a corrente que atravessa a área definida pela amperiana. Como , podemos simplificar a expressão acima e escrever o seguinte
Passo 2
b) Agora, vamos olhar como é o fluxo desse campo através da área da espira . Primeiro, como a barra condutora se move para a esquerda, essa área está aumentando com o tempo, o que significa que o fluxo magnético também está aumentando com o tempo. Então, na espira vai aparecer uma fem induzida e é o que queremos encontrar aqui.
Como o está entrando na página e é perpendicular a ela, podemos colocar o vetor paralelo a , como está na figura abaixo.
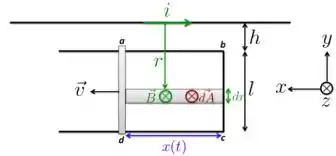
Da expressão que a gente encontrou no Passo 1, vemos que o campo magnético não tem o mesmo valor em todos os pontos da área da espira . Por isso, o fluxo magnético será:
e tiramos o da integral porque tem mesmo valor ao longo da distância . Fazendo a integral acima, chegamos a
O único termo que depende do tempo nessa expressão é . Como , que é a velocidade da barra condutora, o módulo da fem induzida será
Passo 3
c) Como a área está aumentando com o tempo à medida que a barra condutora se movimenta para a esquerda, o fluxo magnético aumenta com o tempo. Por isso, o sentido da corrente induzida que aparece na espira deve ser tal que o campo magnético que ela cria produz um fluxo magnético que se opõe ao fluxo que encontramos.
Por isso, para que haja esse fluxo se opondo a , deve estar circulando na espira no sentido anti-horário.
Resposta
- Sentido anti-horário.