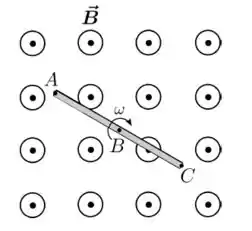
Uma barra condutora fina encontra-se imersa em uma região de campo magnético constante que aponta para fora do plano do papel, como mostrada na figura abaixo. Ela gira com velocidade angular constante em sentido horário em torno de um eixo paralelo à direção do campo e que para por seu centro, que corresponde ao ponto na figura. A barra permanece perpendicular à direção do campo durante todo o movimento. Considerando os pontos , e mostrados na figura, podemos afirmar que, após estabelecido o equilíbrio de cargas no interior da barra, os potenciais elétricos nesses pontos, dados por , e , satisfazem:
Passo 1
Nessa questão, vamos utilizar o desenho na Figura abaixo.
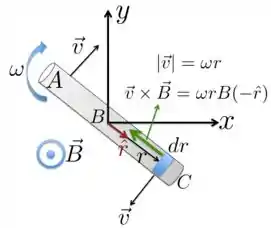
Aqui, como temos uma barra condutora que se move dentro de uma região onde tem campo magnético, então surgirá uma fem induzida dada por
onde é a velocidade do condutor dentro do campo magnético .
Dado o sistema de referência na Figura acima, temos que . Além disso, , que é um vetor radial ao longo da extensão da barra condutora e a velocidade linear tem módulo dado por . Portanto, pontos da barra mais afastados de seu centro possuem velocidades diferentes.
Mas, cuidado!! A velocidade angular de todos os pontos é a mesma e tem valor , beleza? A velocidade linear é que é diferente para pontos diferentes da barra. Fica ligado nisso!!! ;-)
Passo 2
O produto vetorial entre a velocidade e o campo magnético é
que é um vetor na mesma direção de , porém com sentido contrário. Por isso, a fem induzida pode ser escrita como
em que é a distância ao centro de um ponto qualquer da barra condutora e estamos considerando a variável de integração como .
Como a velocidade e o campo magnético são uniformes, ou seja, têm o mesmo valor ao longo da barra, então a fem induzida fica
Portanto, a fem induzida é uma função da distância ao centro da barra. Fica ligado, porque esse resultado vale também para a outra metade da barra. Na Figura que a gente fez aqui, só usamos uma metade da barra para desenhar os vetores, mas o que fizemos é geral, ou seja, se tomássemos a outra parte da barra, também chegaríamos na mesma coisa, sacou?? ;-)
Passo 3
Agora que a gente tem a função fem induzida, podemos avaliar o potencial em cada um dos pontos e da barra condutora. Os pontos e estão à uma distância do centro da barra e, por isso, têm o mesmo potencial cujo valor é
Já o ponto em que , teremos um potencial de
Portanto, a relação entre os potenciais é a seguinte
Resposta
Letra c).