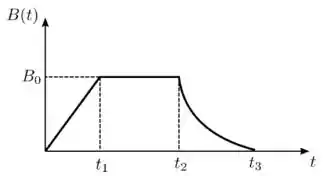
Uma espira condutora circular encontra-se em uma região de campo magnético uniforme, mas não estacionário , que aponta perpendicularmente ao seu plano. A intensidade deste campo varia com o tempo de acordo com o gráfico mostrado abaixo. Os instantes indicados no gráfico são todos positivos e o campo aponta no mesmo sentido durante todo o intervalo indicado. Sobre essa situação, considere as afirmativas abaixo:
- A corrente induzida na espira durante o intervalo é estacionária.
- Não há corrente induzida na espira durante o intervalo .
- As correntes induzidas na espira durante os intervalos e possuem o mesmo sentido.
São VERDADEIRAS as seguintes afirmativas:
- Nenhuma delas
- e
- e
- , e
- e .
Passo 1
Como a espira circular é condutora, para saber se há ou não corrente nela e também quais as características que essa corrente tem, precisamos ver se há ou não variação do fluxo magnético através da área determinada pelo plano da espira e como é o seu comportamento com o tempo.
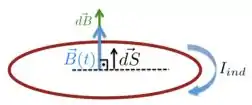
Para entendermos bem as características de , vamos considerar a figura abaixo, em que representamos e o vetor , ambos perpendiculares ao plano da espira.

Para isso, vamos começar olhando para o fluxo magnético de através da área do plano da espira, que é dado por:
O problema disse para gente que o é paralelo ao vetor em todos os pontos do plano da espira. Além disso, para todo instante , o valor do campo é o mesmo em todos os pontos da superfície, ou seja, é uniforme. Colocando essas duas características em , vamos ter
onde é área da espira condutora e tem o mesmo valor durante todo o tempo.
O módulo da fem induzida será, então,
Agora, precisamos ver como é nos diferentes intervalos de tempo do gráfico do enunciado.
Passo 2
No intervalo de tempo , o módulo do campo magnético aumenta linearmente com o tempo. Por isso, podemos escrever que, nesse intervalo, é dado por:
Substituindo em do Passo 1, vamos ter que:
que é independente do tempo, ou seja, a corrente induzida na espira condutora é estacionária durante o intervalo de tempo .
Por isso, o item está CORRETO.
Passo 3
Já no intervalo de tempo , o campo magnético é constante e igual a . Por isso, quando a gente derivar esse cara no tempo, vamos ter uma corrente induzida igual a ZERO.
O item , por essa razão, está CORRETO.
Passo 4
Tanto no intervalo de tempo quanto no , o fluxo do campo magnético é positivo, já que a é sempre paralelo ao vetor área da superfície da espira, como desenhamos na figura do Passo 1.
No entanto, em , o campo está aumentando com o tempo, o que representamos na figura abaixo pelo vetor . Por isso, o fluxo magnético (que é positivo!) também está aumentando com o tempo. Nesse caso, como mostrado na figura abaixo, a corrente induzida tem que estar no sentido horário, se olhamos a espira de cima para baixo:
Já em , (também positivo!) está diminuindo com o tempo de forma que a corrente induzida, pela lei de Lenz, tem que estar no sentido anti-horário, ou seja, tem sentido contrário à do intervalor .
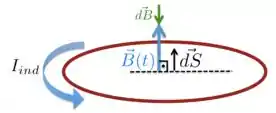
Assim, o item está INCORRETO.
Resposta
Letra h.