Uma barra condutora vertical de comprimento sob ação de uma força externa , se move na horizontal com velocidade constante , deslizando sem atrito sobre 2 condutores paralelos fixos, formando um circuito fechado com uma terceira barra fixa de resistência . Simultaneamente, um fio horizontal infinito está paralelo aos dois condutores e a um distância do condutor mais próximo. Por este fio passa uma corrente constante no sentido negativo do eixo . Sabendo que o módulo do campo magnético produzido por um fio com corrente a uma distância é dado por , determine:
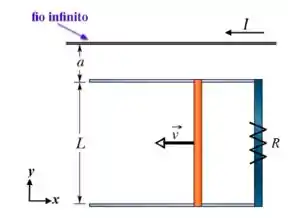
- O módulo da força eletromotriz induzida no circuito.
- O sentido da corrente induzida no circuito e justifique sua resposta.
- Determine o vetor força externa , em termos dos parâmetros geométricos do problema e demais dados no enunciado.
Passo 1
a) Bom, primeiro, é sempre importante entendermos o que está acontecendo aqui neste problema para depois passar para as contas. A corrente que passa no fio infinito produz um campo magnético que atravessa a área da espira da figura abaixo. Essa área aumenta à medida que a barra condutora vertical se desloca para a esquerda.
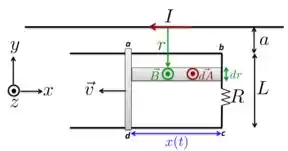
Se a área aumenta com o tempo, então o fluxo do campo magnético também aumenta e, por isso, teremos uma fem induzida no circuito e isso que queremos calcular agora. “Bora” lá?
Vamos calcular o fluxo magnético . O campo magnético gerado por atravessa uma área , em que colocamos o vetor paralelo ao campo , ou seja, ambos perpendiculares à página e saindo dela, como está na figura acima. Com isso, o fluxo magnético fica
Como não varia ao longo da direção de , então podemos tirar da integral esse termo. Fazendo isso, teremos
Agora sim podemos encontrar o valor do módulo da fem
onde já usamos que é a velocidade constante com que a barra condutora se desloca para a esquerda.
Passo 2
b) Como comentamos no Passo 1, a área pela qual o campo passa aumenta com o tempo e por isso, pela lei de Lenz, a corrente induzida que aparece na espira deve estar no sentido horário. Com isso, o campo induzido gerado por atravessa a área da espira e o fluxo magnético correspondente se opõe à taxa temporal de variação do fluxo do campo magnético gerado por .
Passo 3
c) Como mostra a figura acima, a corrente induzida tem sentido horário e, como o campo gerado por está saindo da página, a força infinitesimal sobre um comprimento da barra será
e como , a força será
que está apontando para a direita.
Por isso, a força externa total é , que deve ser aplicada à barra para que ela tenha velocidade constante para a esquerda. Por isso, utilizando a expressão acima e integrando, teremos:
Resolvendo a integral,
que mostra que a força externa total tem mesma direção, mesmo módulo, porém sentido contrário ao da força .
Agora vamos colocar essa força em termos dos parâmetros geométricos que o item pede.
Como , a corrente induzida é
Reescrevendo a força externa total ,
Resposta
- Corrente induzida no sentido horário ;