Uma bobina retangular com voltas, de lados e e resistência total , está contida no plano e gira com velocidade angular em torno do eixo . Esta bobina é atravessada por um campo magnético de módulo dirigido ao longo do eixo , como mostrado na figura . A rotação é iniciada de modo que o plano da bobina seja perpendicular à direção de em .
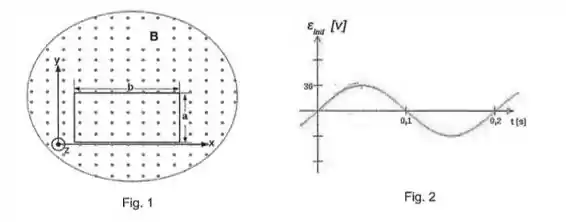
A figura mostra o comportamento da tensão induzida na bobina em função do tempo. Utilizando a figura e os outros dados do problema, encontre:
(a) O número de voltas da bobina retangular;
(b) A taxa máxima de variação do fluxo magnético através da bobina;
(c) O valor da corrente induzida e seu sentido (horário ou anti-horário) na bobina quando ;
(d) A potência média dissipada no resistor.
(Sugestão: em todos os cálculos use )
Passo 1
a) Sabemos, pela lei de Lenz, que:
E sabemos também que:
Onde o ângulo , sendo a rotação angular, logo:
Portanto:
Quando , a tensão induzida também é nula, o que coincide com o gráfico da Figura 2.
Para descobrir o número de voltas, vamos usar o dado da Figura 2, que nos dá o valor máximo da tensão induzida.
Através do gráfico da Figura 2 vemos que o primeiro ponto em que a tensão induzida é nula ocorre em , logo:
Como o produto é sempre constante:
Dessa forma, atingiremos o valor máximo do fluxo quando o ângulo for , e:
Logo:
Passo 2
b) A taxa máxima pode ser encontrada facilmente pela Figura 2:
Passo 3
c) Quando , pela Figura 2, a bobina estará com sua tensão induzida máxima, portanto:
Logo:
Analisando a fórmula:
Nesse instante a tensão induzida é positiva, logo, a variação do fluxo será negativa.
Assim, de acordo com a Lei de Lenz, a corrente induzida terá um sentido de forma que o campo magnético auto induzido tende a “ajudar” o campo externo, tendo a mesma direção e sentido.
Utilizando a regra da mão direita, vemos que para isso ser possível, a corrente induzida deve estar no sentido anti-horário.
Passo 4
d) A potência média é dada por:
Portanto, como temos a expressão de :
Como e:
Substituindo lá:
Logo:
Resposta
a)
b)
c) no sentido anti-horário.
d)