Considere dois circuitos fechados ôhmicos, 1 e 2, puramente resistivos, de mesma resistência , no plano cartesiano , muito afastados um do outro, com a forma de um “oito” torcido, de modo que, para o circuito , suas partes, de baixo e de cima, têm a mesma área , ao passo que, para o circuito , a área da parte de baixo continua sendo , mas aquela da de cima é o triplo. Tais circuitos estão sujeitos ao campo magnético , com . Assinale a alternativa que melhor indica quais são os módulos das intensidades de corrente induzida em tais circuitos e as correspondentes orientações nas suas partes de cima.
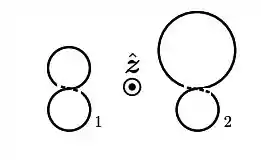
(a) , horário.
(b) , anti-horário.
(c) , horário; , horário.
(d) , anti-horário; , anti-horário.
(e) , horário; , horário.
(f) , anti-horário; , anti-horário.
Passo 1
Conforme a Lei de Lenz
Como .
Para o circuito 1, a parte de cima tem área , e, portanto, a força eletromotriz que é criada na parte de cima é dada por:
Mas esta força eletromotriz irá aparecer nessa parte de cima induzindo uma corrente em qual sentido? É só usar a regra da mão direita, percebendo que o fluxo cresce saindo do papel e, portanto, a corrente irá fluir no sentido horário.
E para a parte debaixo? O que vai acontecer? A mesma ideia! Uma fem irá nascer induzindo uma corrente também no sentido horário.
Temos duas correntes então: uma no sentido horário na parte de cima e outra no sentido horário na parte de baixo.
O que acontece é que as duas irão se anular por que, como o fio é torcido, elas estão indo uma contra a outra.
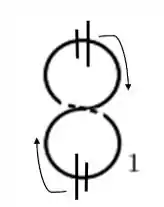
Portanto:
Passo 2

Para o circuito 2, o pensamento é o mesmo, no entanto, a fem induzida na parte superior é maior, já que a área é o triplo da de baixo, se liga:
E
Conforme o esquema acima, as correntes geradas ainda estão indo uma contra a outra. Como a da parte de cima é maior a corrente resultante é:
Ambas as correntes estarão no sentido horário porque o fluxo está aumentando, então as correntes precisam compensar esse aumento.
Resposta
(a)