Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Lenz

Ver Teoria
Exercício 34123456789101112131415161718192021222324252627282930313233353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697

Enunciado

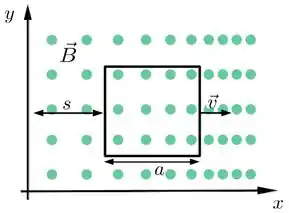
A figura mostra uma espira condutora quadrada de lado a , localizada no plano x y . A espira desloca-se ao longo do eixo x com velocidade de módulo v = d s / d t , onde s é a distância da extremidade esquerda da espira ao eixo y . Tal espira está submetida a um campo magnético variável no espaço e aponta para fora do plano da página e cujo módulo é dado por B x = α x , onde α é uma constante positiva. Nestas circunstancias, determine:

(a) O módulo do fluxo magnético através da espira

(b) O módulo da força eletromotriz induzida na espira

(c) O sentido de circulação da corrente induzida (horário ou anti-horário). Justifique a sua resposta.

Passo 1

Temos que o fluxo magnético sobre a espira é dado por

Φ B = ∫ B → . d A →

Onde B → é o nosso campo magnético que está entrando na folha e d A → é o vetor perpendicular ao elemento de área da espira.

Como a espira está no plano x y , esse vetor de elemento de área aponta na direção fora do plano e é paralelo ao campo magnético. Isso implica que o produto escalar, B → . d A → , vira o produto B d A .

Aqui eu fiz com que B → e d A → tivessem o mesmo sentido de forma que Φ B > 0 . Já que o enunciado pede o módulo do fluxo isso não será problema!

Como vamos integrar ao longo dessa espira quadrada, o nosso elemento de área será dado por d A = d x d y e os limites de integração mostrados abaixo

Φ B = ∫ s s + a d x B ( x ) ∫ 0 a d y

Onde eu setei y = 0 na face de baixo do quadrado. Assim fazendo essas integrais (lembrando que B ( x ) = α x

Φ B = ∫ s s + a d x B ( x ) ∫ 0 a d y = α ∫ s s + a x d x ∫ 0 a d y = α x 2 2 s s + a a

Φ B = α a 2 s + a 2 - s 2

Calculando o termo entre colchetes temos

Φ B = α a 2 2 a s + a 2

Φ B = α a 2 s + α a 3 2

Passo 2

Temos que, pela lei de Faraday, o módulo da força eletromotriz induzida é dado por

ε = d Φ B d t = d d t α a 2 s + α a 3 2

Como no fluxo a única variável que varia no tempo é s  

ε = α a 2 d s d t

Como d s / d t = v

ε = α a 2 v

Passo 3

Vemos que com o passar do tempo a espira vai para uma região onde o campo magnético é mais intenso, o que significa que o fluxo do campo magnético aumenta com o tempo.

Se o fluxo do campo magnético aumenta com o tempo, temos que, pela lei de Lenz, a corrente induzida gerará um campo magnético contrário ao campo magnético externo, ou seja, apontando para dentro da página.

Para gerar um campo que entre na página é necessário que a corrente induzida circule no sentido horário.

Repostas

a) Φ B = α a 2 s + α a 3 2

b) ε = α a 2 v

c) Horário

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

20- Uma barra metálica com 1.50m de comprimento é puxada para a direita a 5.0m / s regulares e perpendicularmente a um campo magnético uniforme de 0.750T . A barra desliza sobre trilhos metálicos para
17- Use a lei de Lenz para determinar o sentido da corrente induzida que passa no resistor a b indicado na Figura 29.33 , quando ( a ) a chave S é aberta depois de ficar fechada durante alguns minutos
15- Um anel circular está em uma região do espaço onde existe um campo magnético uniforme, como indica a Figura 29.31 . O campo magnético está entrando no plano da figura. Determine o sentido (horário
18- Um tubo de papelão é circundado por dois enrolamentos feitos com dois fios isolados, formando espiras em sentidos contrários, como indica a Figura 29.34 . Os terminais a e b do enrolamento A podem
16- A corrente na Figura 29.32 obedece a equação I t = I 0 e - b t . Em que b0 . Determine o sentido (horário ou anti-horário) da corrente induzida na bobina redonda para t0 .