A figura abaixo mostra uma espira quadrada de lado e resistência elétrica , que encontra-se nas proximidades de um fio infinito retilíneo, percorrido por uma corrente elétrica constante . O fio é direcionado paralelamente aos lados verticais da espira quadrada. Note que o fio e a espira são coplanares. Sabe-se que a espira desloca-se com velocidade constante , na direção perpendicular ao fio. A distância do fio infinito à extremidade esquerda da espira é dada por . Note que é uma função do tempo. Todo o sistema está imerso no vácuo, cuja constante de permeabilidade magnética é dada por .
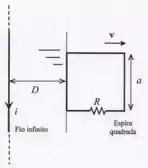
- Calcule o módulo do fluxo magnético gerado pelo campo magnético do fio infinito através da espira.
- Calcule o módulo e o sentido (horário ou anti-horário) da corrente elétrica induzida na espira.
- Neste item, responda às mesmas perguntas feitas no item b), agora supondo que a espira se move com velocidade paralela ao fio infinito (observe que neste caso a distância não varia com o tempo).
Passo 1
a) Pela regra da mão direita, o campo magnético produzido pela corrente está saindo do plano da espira e é perpendicular à página. Como a espira se move para a direita, o fluxo magnético através da espira varia com o tempo, o que vai resultar em uma fem induzida na espira e como ela tem resistência, também vai passar por ela uma corrente induzida.
Para gente ver primeiro como é o fluxo magnético, vamos olhar para a figura abaixo, que tem o elemento de área .
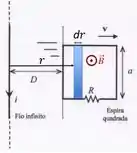
O módulo do campo magnético produzido por passando nesse fio infinito é dado por:
expressão que obtemos utilizando a lei de Ampère.
Podemos escolher o vetor área saindo da página e, portanto, paralelo ao campo magnético. Isso facilita as contas, porque vamos poder escrever o fluxo magnético da seguinte forma:
que depende do tempo porque a distância está variando no tempo.
Resolvendo a integral, teremos:
Vamos reescrever essa expressão para ficar mais fácil no próximo item:
Passo 2
b) Como o fluxo magnético varia com o tempo, vai aparecer na espira uma fem induzida dada por
Derivando o primeiro termo de do Passo 1, temos:
já que a taxa temporal com que a distância varia é exatamente a velocidade . Fazendo a mesma coisa com o segundo termo de , vamos ter
Como definimos o vetor área saindo da página e perpendicular a ela, o sentido positivo, dado pela regra da mão direita para , será anti-horário. Por isso, como , a fem induzida e, portanto, a corrente induzida, estarão no sentido anti-horário.
Passo 3
c) Como a espira caminha com velocidade constante paralela ao fio, todos os seus pontos estarão sempre à mesma distância da corrente , o que significa que o fluxo magnético será o mesmo em todo tempo: . Portanto,