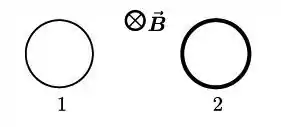
Considere dois anéis circulares em repouso: um condutor e outro isolante . Ambos estão sujeitos a campos magnéticos não estacionários orientados para dentro do plano dos anéis. Quanto ao campo elétrico induzido e à corrente elétrica induzida , nos anéis, podemos afirmar que:
- , ; ,
- , ; ,
- , ; ,
- , ; ,
- , ; ,
Passo 1
Como temos campos magnéticos não estacionários, temos fluxos magnéticos não estacionários. Pela Lei de Faraday:
Como a Lei não diz respeito à nenhum material específico, ela deve ser válida em ambos os casos e .
Passo 2
Seguindo, pela definição de força eletromotriz:
Como determinamos que vai existir fem em ambos os casos, temos que o campo elétrico vai ser não nulo em ambos os casos também:
Então temos que:
Já matamos um monte de alternativas, mas nem vale a pena ficar vendo quais... Vamos seguir nossa análise.
Passo 3
Em seguida ele quer saber das correntes. Pela Lei de Ohm:
Num material condutor vai existir corrente sem problemas. Portanto:
Passo 4
Já num isolante, por definição, temos algo do tipo:
Logo:
Portanto, sendo “bastante” rigorosos matematicamente:
Resposta
Letra c