Considere uma superfície formada por três quadrados de lado : e , como é mostrado na figura. O quadrado é paralelo ao plano . Na região da superfície existe um campo magnético uniforme .
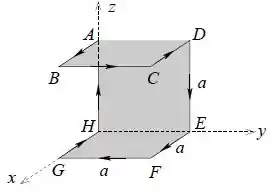
- Calcule o fluxo magnético através da superfície para .
- Calcule o fluxo magnético através da superfície para .
- Considere com . Calcule a integral de linha do campo elétrico ao longo do caminho fechado na fronteira de percorrido no sentido indicado na figura.
Passo 1
- Calcule o fluxo magnético através da superfície para .
- Calcule o fluxo magnético através da superfície para .
- Considere com . Calcule a integral de linha do campo elétrico ao longo do caminho fechado na fronteira de percorrido no sentido indicado na figura.
O fluxo magnético é dado por:
Nesse caso, como é constante:
Vamos determinar o sentido do vetor através da regra da mão direita, acompanhando o sentido da corrente.
Assim, usando a regra da mão direita, vemos que, para cada plano, terá os seguintes sentidos:
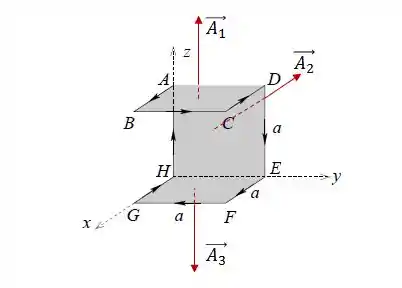
O fluxo magnético total será:
Passo 2
Beleza! Aqui é o mesmo esquema de antes.
Passo 3
O problema nos pede para calcular
Mas, na verdade... nós podemos associar essa integral com a Lei de Faraday. Dá uma olhada:
Nós já calculamos o fluxo magnético para no passo anterior. Nós tínhamos encontrado que:
Show! O problema nos disse que . Logo:
Agora podemos voltar para Lei de Faraday: