A figura abaixo mostra uma espira quadrada de lado que move-se da esquerda para a direita com aceleração constante (). A espira penetra em uma região do espaço em que há um campo magnético constante (), perpendicular ao plano da folha e apontando para dentro. A espira tem resistência . Nessa figura, a variável mede a posição do lado direito da espira com relação à fronteira da região de campo e é uma função do tempo . Suponha que no instante e que a espira parte do repouso.
OBS: Suas respostas devem ser dadas em função apenas de , , e .
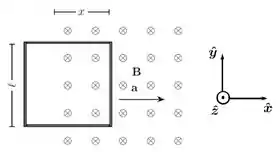
- Determine a intensidade do fluxo de campo magnético através da área definida pela espira como função do tempo , considerando os intervalos em que a espira está entrando no campo e depois que ela está totalmente imersa.
- Determine a intensidade e o sentido da corrente induzida na espira como função do tempo , considerando os mesmos intervalos.
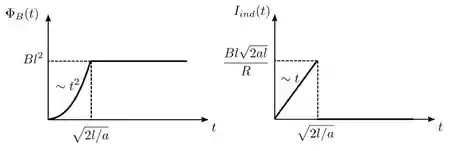
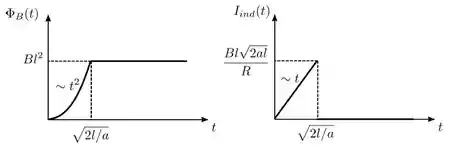
- Faça gráficos da intensidade do fluxo e da corrente induzida como função do tempo , destacando os pontos relevantes.
Passo 1
a)A espira se move com aceleração constante, então a equação da coordenada deve ser escrita como
Então, isolando na equação acima, o tempo que a espira leva pra entrar no campo é (lembrando que nesse caso, , já que é o comprimento da espira).
Como o enunciado pede pra considerar os intervalos em que a espira está entrando no campo e quando já está lá dentro, vamos calcular 2 fluxos magnéticos: um para e outro para .
A fórmula de fluxo magnético é assim
Como a área da espira é plana e o campo magnético é constante, a gente pode escrever simplesmente:
é o ângulo entre e . Vamos orientar o vetor na mesma direção do campo, assim temos que:
Onde é a porção da espira que está imersa no campo no tempo .
Passo 2
b)Então vamos calcular o fluxo magnético para cada intervalo de tempo:
I)
Nesse intervalo, a área da espira que está imersa no campo é
Então:
II)
Como agora a espira está totalmente imersa no campo
Então o fluxo magnético será
Passo 3
c)A gente consegue usar a Lei de Faraday pra determinar a força eletromotriz nos dois intervalos, lembrando que ela é dada por
Depois podemos, então, calcular a corrente induzida dividindo pela resistência .
I)
Nossa força eletromotriz deu negativa, isso quer dizer que seu sentido é contrário à regra da mão direita a partir do vetor área (sentido horário). Então tanto a força eletromotriz quanto a corrente induzida vão ter sentido anti-horário.
II)
Nesse caso, a força eletromotriz deu 0 porque o fluxo de campo magnético é constante. Então, nossa corrente induzida também vai ser 0.
Passo 4
c)Os gráficos são mostrados na figura abaixo.
Repare que antes da espira entrar totalmente no campo magnético, o fluxo magnético tem comportamento quadrático enquanto a corrente induzida tem comportamento linear. Já quando a espira entra totalmente no campo, o fluxo magnético é constante e a corrente induzida é nula.
Resposta
- no sentido anti-horário
C)