Um pedaço de fio condutor ôhmico isolado é torcido de modo a constituir um circuito em forma de oito. Por razão de simplicidade, modele as duas metades da figura de oito como circunferências de círculo. O raio do círculo superior é e o do inferior é . O circuito completo é puramente resistivo (com capacitância e autoindutância desprezíveis), tendo resistência . A partir de um campo magnético uniforme mas não estacionário
Onde é aplicado perpendicularmente ao plano dos dois circuitos, conforme mostrado na figura.
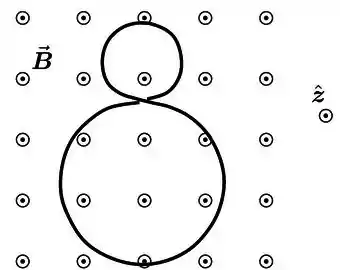
- Para determino o fluxo total através do circuito.
- Para determine o sentido da corrente elétrica induzida ao longo do fio indicando-o claramente em cada uma das circunferências, seja por intermédio de uma seta, seja pelas expressões horário ou anti-horário.
- Para determine o módulo da intensidade da corrente elétrica induzida no fio.
Passo 1
O fluxo é dado pela integral:
Onde é a superfície toda do circuito. Note que quando ele pega um arame normal e “torce” ele passa a ter duas orientações do normal:
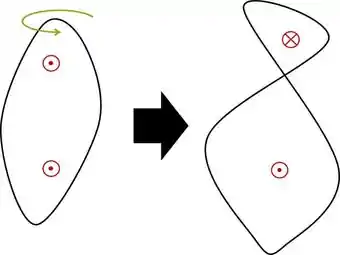
Fazendo o fluxo, podemos separar em duas integrais, onde cada uma tem um vetor normal constante. Seja a de raio maior a com e a outra no sentido de .
Pondo as constantes (digo constantes em relação às variáveis de integração, que são de espaço) para fora:
Segue:
Podemos ver que o fluxo total aumenta com o tempo.
Passo 2
Pela Lei de Lenz, como temos um fluxo aumentando no sentido de , o efeito induzido vai tentar compensar este fato. Por conta disto, pela regra da mão direita podemos ver que será induzida uma corrente que, no círculo maior, é horária:
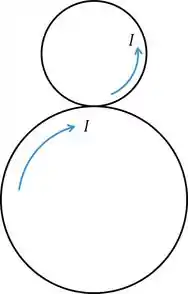
Naturalmente, no menor vai ser anti-horária.
Passo 3
Para calcular a intensidade da corrente induzida vamos rodar a Lei de Faraday:
E juntar com a Lei de Ohm:
De forma que:
Derivando o fluxo:
O módulo da corrente fica então:
Resposta
a)
b)
Anti-horária no menor e horária no maior.
c)