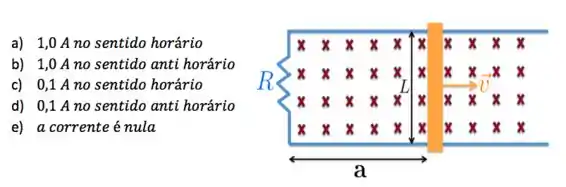
A figura abaixo mostra um bastão condutor de comprimento sendo puxado ao longo dos trilhos condutores com velocidade constante de . Todo o sistema está imerso em um campo magnético perpendicular entrando na página e de módulo igual a . Sabendo que a resistência total do circuito é , a corrente induzida e o seu sentido são, respectivamente
Passo 1
Vamos identificar com cuidado os aspectos principais dessa problema. Primeiro, temos um condutor que se desloca com velocidade para a direita sobre trilhos, também condutores e o sistema todo tem uma resistência .
O campo magnético é constante em todo o espaço e é sempre perpendicular à área do circuito. Esta área, por sua vez, aumenta com o tempo, já que o bastão condutor se desloca para direita. Então olha só, já sabemos que haverá uma fem induzida no circuito e que édevida à variação do fluxo magnético com o tempo: a variação da área em função do tempo é , já que é uma função do tempo!
Passo 2
Uma vez identificados esses aspectos, vamos escrever um pouco de matemática agora. Para isso, podemos colocar o vetor área paralelo ao vetor , portanto também está entrando no plano da página. Por isso, o fluxo magnético fica:
Agora, é exatamente a velocidade com que o bastão se desloca para a direita: . Disso, o módulo é:
Essa corrente tem que ter o sentido antihorário, pois, à medida que o bastão se desloca para a direita, o fluxo magnético aumenta e essa corrente produzirá um campo cujo fluxo está em sentido oposto àquele fluxo original.
Passo 3
Substituindo os valores numéricos do enunciado:
que é o valor pedido pelo problema.
Resposta
Portanto, letra d).