Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Lenz

Ver Teoria
Exercício 61234578910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697

Enunciado

Uma região circular no plano x y é atravessada por um campo magnético uniforme orientado no sentido positivo do eixo z . O módulo B do campo (em teslas) aumenta com o tempo t (em segundos) de acordo com a equação B = a t , onde a é uma constante.

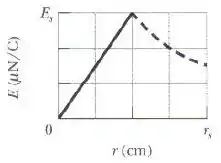
A figura acima mostra o módulo E do campo elétrico criado por esse aumento do campo magnético em função radial r ; a escala do eixo vertical é definida por E s = 300   μ N / C , e a escala do eixo horizontal é definida por r s = 4,0   c m .

Determine o valor de a .

Passo 1

Pela Lei de Faraday, temos que:

∮ E → ∙ d s → = - ∂ ϕ B ∂ t

Como a área é constante e o campo magnético é uniforme, podemos reescrever a equação acima da seguinte forma:

∮ E → ∙ d s → = - A ∂ B ∂ t

Como estamos calculando o campo elétrico induzido no interior do solenóide, a área transversal será um círculo, e a curva fechada que usaremos na integral é a curva circular que contorna A . Logo, podemos reescrever a equação acima da seguinte forma:

E 2 π r = - π r 2 ∂ B ∂ t

E = - r 2 ∂ B ∂ t

E = r 2 ∂ B ∂ t

Onde, entre 0 < r < 2   c m :

∂ B ∂ t = a

Logo:

E = a r 2

Passo 2

Para r = 2   c m , E = 300   μ N / C , logo:

300 × 10 - 6 = 2 × 10 - 2 × a 2

a = 0,03   T / s

Resposta

a = 0,03   T / s

Exercícios de Livros Relacionados

20- Uma barra metálica com 1.50m de comprimento é puxada para a direita a 5.0m / s regulares e perpendicularmente a um campo magnético uniforme de 0.750T . A barra desliza sobre trilhos metálicos para
17- Use a lei de Lenz para determinar o sentido da corrente induzida que passa no resistor a b indicado na Figura 29.33 , quando ( a ) a chave S é aberta depois de ficar fechada durante alguns minutos
15- Um anel circular está em uma região do espaço onde existe um campo magnético uniforme, como indica a Figura 29.31 . O campo magnético está entrando no plano da figura. Determine o sentido (horário
18- Um tubo de papelão é circundado por dois enrolamentos feitos com dois fios isolados, formando espiras em sentidos contrários, como indica a Figura 29.34 . Os terminais a e b do enrolamento A podem
16- A corrente na Figura 29.32 obedece a equação I t = I 0 e - b t . Em que b0 . Determine o sentido (horário ou anti-horário) da corrente induzida na bobina redonda para t0 .