Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Lenz

Ver Teoria
Exercício 18123456789101112131415161719202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697

Enunciado

Lei de Faraday, Lei de Lenz

Uma espira retangular tem comprimento a , largura b e resistência R .

Suponha que numa região do espaço exista um campo magnético que cresce linearmente com y , isto é, aumenta à medida que se afasta de y a partir da origem, e é dado por B y = C y , onde C é uma constante. Este campo magnético está na direção de - z ^ (”entrando no plano da página”).

A espira é então imersa nessa região, como mostra a figura abaixo, onde y é a distância do centro da espira até o eixo x .

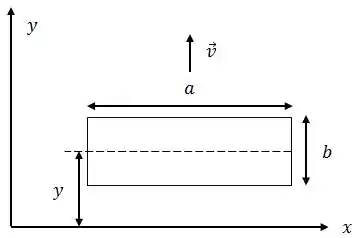
Determine:

  1. O fluxo do campo magnético através da espira.
  2. A corrente induzida na espira à medida que esta se afasta do eixo x com velocidade constante v ao longo de y .
  3. O sentido da corrente induzida na espira (justificar a resposta).

Passo 1

  1. O fluxo do campo magnético através da espira.

    2. Por definição, o fluxo magnético é dado por:

    ϕ B = ∬ S B → ∙ d A →

    Podemos dizer que d A = a d y ' . Onde y ' vai variar de y - b / 2   até y + b / 2

    Substituindo a expressão pro campo magnético que o problema nos deu:

    ϕ B = C a ∫ y - b / 2 y + b / 2 y ' d y '

    ϕ B = C a y ' 2 2 y - b / 2 y + b / 2

    ϕ B = C a 2 y + b 2 2 - y - b 2 2

    ϕ B = C a 2 2 y b

    ϕ B = C y a b

    Passo 2

  2. A corrente induzida na espira à medida que esta se afasta do eixo x com velocidade constante v ao longo de y .

    3. Vamos lá... para encontrar a corrente induzida, precisamos calcular primeiro a fem induzida, para que possamos utilizar a fórmula:

    I = ε R

    Para calcular a fem induzida, podemos usar a lei de Faraday:

    ε = - ∂ ϕ [ B ] ∂ t

    Conforme a espira se afasta do eixo x , o valor de y varia. Já que a velocidade é constante, podemos dizer que:

    y = v t

    Então podemos reescrever o fluxo do campo magnético como:

    ϕ B = C v a b t

    A fem induzida, por sua vez, será, em módulo:

    ε = ∂ ϕ B ∂ t

    ε = C v a b

    Agora sim podemos encontrar uma expressão para a corrente induzida:

    I = ε R

    I = C v a b R

    Passo 3

  3. O sentido da corrente induzida na espira (justificar a resposta).

A lei de Lenz nos diz o seguinte:

O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.

É o seguinte... se o fluxo magnético está aumentando, a corrente induzida está no sentido anti-horário. Se o fluxo magnético está diminuindo, a corrente induzida está no sentido horário.

Vamos analisar o fluxo magnético.

ϕ B = C y a b

Conforme o tempo passa, o valor de y aumenta, aumentando, também, o fluxo do campo magnético. Assim, a corrente induzida estará no sentido anti-horário.

Resposta

a.

ϕ B = C y a b

b.

I = C v a b R

c.

A corrente induzida estará no sentido anti-horário.

Exercícios de Livros Relacionados

20- Uma barra metálica com 1.50m de comprimento é puxada para a direita a 5.0m / s regulares e perpendicularmente a um campo magnético uniforme de 0.750T . A barra desliza sobre trilhos metálicos para
17- Use a lei de Lenz para determinar o sentido da corrente induzida que passa no resistor a b indicado na Figura 29.33 , quando ( a ) a chave S é aberta depois de ficar fechada durante alguns minutos
15- Um anel circular está em uma região do espaço onde existe um campo magnético uniforme, como indica a Figura 29.31 . O campo magnético está entrando no plano da figura. Determine o sentido (horário
18- Um tubo de papelão é circundado por dois enrolamentos feitos com dois fios isolados, formando espiras em sentidos contrários, como indica a Figura 29.34 . Os terminais a e b do enrolamento A podem
16- A corrente na Figura 29.32 obedece a equação I t = I 0 e - b t . Em que b0 . Determine o sentido (horário ou anti-horário) da corrente induzida na bobina redonda para t0 .