A figura abaixo mostra um trilho condutor com forma de e de resistência desprezível sobre o qual uma barra curva, na forma de um semicírculo de raio , desliza sem atrito e com velocidade constante . Todo o sistema está sobre o plano e sob a ação de um campo magnético constante . A barra curva possui resistividade e seção transversal constante de área . Nos cálculos abaixo, escolha o vetor unitário normal ao plano definido pela barra curva e o trilho condutor como .
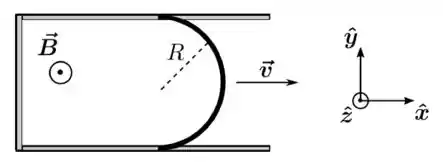
- Determine a intensidade e o sentido da corrente induzida na barra em movimento.
- Determine a força magnética (módulo, direção e sentido) que o campo magnético exerce sobre a barra devido à corrente induzida.
Passo 1
a) Para resolvermos essa questão, vamos considerar que o vetor área é e, portanto, está na mesma direção e sentido do campo magnético , como está mostrado na Figura abaixo.
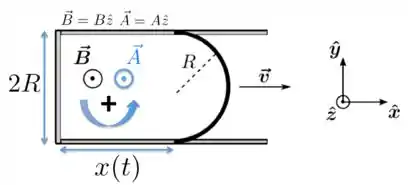
Como colocamos o vetor área nessa direção, então, pela regra da mão direita, o sentido positivo para a corrente será o anti-horário, como indicamos na Figura com uma seta e com o sinal . Então, depois de fazermos as contas, vamos ver o sinal da corrente induzida .
Da Figura acima, vemos que área pode ser escrita como
Agora vamos olhar para o fluxo magnético . Como o problema diz que o campo é constante, e colocamos paralelo à , então temos que o fluxo é
Substituindo a expressão para , temos
que depende do tempo, porque o comprimento está aumentando com o tempo.
Bom, se o fluxo está mudando com o tempo, então esperamos que apareça uma fem induzida . Vamos calcular isso agora...
Passo 2
a) Continuação...
A fem induzida é
Como o segundo termo dentro do parênteses é constante no tempo e , que é a velocidade da barra semicircular, a fem induzida é
Portanto, como a fem induzida é negativa, a corrente induzida estará no sentido horário, contrário ao sentido positivo ilustrado na Figura.
Falta ainda obtermos o valor dessa ...Não desanima!!
Agora, como a barra tem resistividade , seção transversal e comprimento , e sendo um condutor ôhmico, então sua resistência é dada por
A corrente induzida será, então,
que está no sentido horário.
Passo 3
b) Como o campo magnético é uniforme, então, a força magnética atuando sobre a barra semicircular é
Portanto, precisamos calcular a integral para a barra semicircular. Para isso, considere a Figura abaixo.
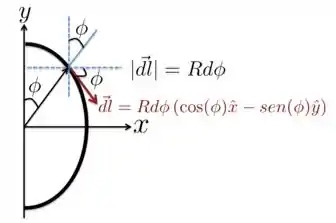
Na Figura, escrevemos o vetor em termos de suas componentes ao longo dos eixos e . Repare que, como a corrente está no sentido horário, então o vetor deve ser tangente à barra em todos os pontos e deve ter o sentido e direção dados pela corrente naquele ponto. Por isso, desenhamos apontando para baixo na Figura!! Fica ligado nisso, porque a direção e sentido desse vetor depende do sentido da corrente. Beleza??
Se a gente integra o vetor , temos
já que a primeira integral logo depois da primeira igualdade é nula. Portanto, substituindo esse resultado na força , teremos
Como e substituindo que encontramos no item a), teremos que
Resposta
a) sentido horário;
b)