Uma espira circular de raio r está imersa em um campo magnético uniforme e estacionário
. Ela gira com velocidade angular constante em torno do eixo de um sistema de coordenadas, conforme a figura abaixo. Considere que, no instante , a espira encontra-se sobre o plano , centrada na origem, e o seu vetor área aponta no mesmo sentido do campo. Sobre essa situação, considere as afirmativas abaixo:
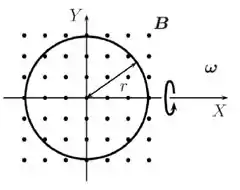
(I) O fluxo de campo magnético através da espira varia com o tempo na forma .
(II) A força eletromotriz induzida na espira é máxima no instante .
(III) O sentido da corrente induzida na espira é sempre anti-horário quando visto da direção positiva para a negativa no eixo .
São VERDADEIRAS as afirmativas:
(a) Apenas I
(b) Apenas II
(c) Apenas III
(d) Apenas I e II
(e) Apenas I e III
(f) Apenas II e III
(g) I, II e III
(h) Nenhuma delas
Passo 1
Vamos analisar cada uma das afirmativas:
I) Verdadeira. O fluxo magnético vai ser:
Mas e . Como é constante, podemos tirar da integral também, logo:
Passo 2
II) Falsa. A força eletromotriz é dada por
A força eletromotriz será máxima quando for máximo. Isso vai acontecer quando
Passo 3
III) Falsa. Observe que, por exemplo, para , a corrente está no sentido horário.
Logo, a alternativa correta é a letra A.
Resposta
(a) Apenas I