Halliday - Vol. 3 – 9º edição – Capítulo 30 – Seção 4 – Exercício 27
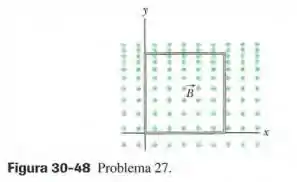
(Capítulo 30.4 – Exercício 27) Na Fig. 30-48, uma espira quadrada com de lado é submetida a um campo magnético, dirigido para fora do papel, cujo módulo é dado por , onde está em teslas, em segundos e em metros. Determine (a) o valor absoluto e (b) o sentido da força eletromotriz induzida na espira no instante .
Passo 1
Fala pessoal! A questão fornece uma espira quadrada de lado com um campo magnético perpendicular (saindo da figura) que depende do tempo e da coordenada . E aí queremos calcular o valor e o sentido da força eletromotriz em
O primeiro passo é calcular o fluxo sobre a espira. Para isso, vamos adotar com convenção a normal saindo do plano da figura. Assim, o fluxo magnético será positivo pois o campo aponta para fora da figura na direção positiva.
A fem induzida é calculada assim
O fluxo em uma faixa horizontal fina de espessura será
Passo 2
Assim,
Portanto,
Passo 3
Pela lei de Faraday, a fem induzida é
Assim, para e :
Em valor absoluto:
Passo 4
No item (b) devemos dizer qual o sentido da fem induzida. Por convenção, adotamos a normal à região limitada pela espira para fora da figura (direção positiva), de modo que o sentido positivo da fem seria o anti-horário.
Como obtivemos : sentido horário!
Resposta
Sentido horário