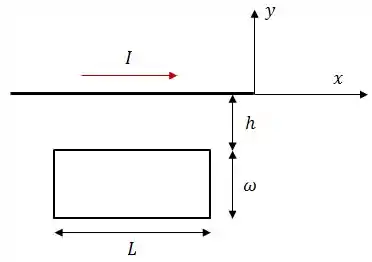
A figura abaixo mostra uma espira retangular, de largura e comprimento , e um fio longo que transporta uma corrente de acordo com a disposição da figura. A distância do fio ao lado maior da espira é .

Determine:

O fluxo magnético através da espira;

Suponha agora que a corrente varie com o tempo de acordo com a expressão , onde e são constantes. Detemine:

A fem induzida na espira, se , e ;

O sentido da corrente induzida (explicar);

A fem induzida na espira, se e e ;

De acordo com a Lei de Faraday, a fem induzida é definida por:

Logo, como a única coisa que varia na fórmula do fluxo magnético é a corrente:

O enunciado nos disse que , logo .

Onde , e .

A fem induzida em módulo será:

O sentido da corrente induzida (explicar);

De acordo com a Lei de Lenz:

O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.

Simplificando... a corrente induzida é sempre do contra, se o fluxo magnético através da espira estiver aumentando, a corrente induzida vai gerar um campo magnético no sentido contrário, só pra atrapalhar... se o fluxo magnético estiver diminuindo, a corrente induzida vai gerar um campo magnético a favor.

Aqui, o campo magnético gerado pelo fio, sobre a espira, tem sentido entrando na página, conseguiu ver?

Esse campo magnético é dado por:

Assim, como a área é constante, o fluxo magnético vai variar somente se o campo magnético variar. Como a corrente está aumentando , o campo magnético vai aumentar e, logo, o fluxo magnético também vai aumentar.

Assim, a corrente induzida vai gerar um campo que se oponha a esse aumento. Como o campo magnético na espira tem sentido entrando na página... o campo magnético induzido vai ter sentido saindo da página.

Pela regra da mão direita, para que o campo magnético gerado pela corrente induzida esteja saindo da página, a corrente induzida deve estar no sentido anti-horário.