Halliday - Vol. 3 – 9º edição – Capítulo 30 – Seção 4 – Exercício 15
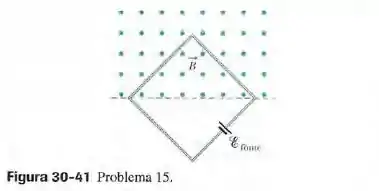
(Capítulo 30.4 – Exercício 15) Uma espira quadrada com de lado é mantida perpendicular a um campo magnético uniforme com metade da área da espira na região em que existe campo, como mostra a figura 30-41. A espira contém uma fonte ideal de força eletromotriz . Se o módulo do campo varia com o tempo de acordo com a equação , com em teslas e em segundos, determine (a) a força eletromotriz total aplicada à espira e (b) o sentido da corrente (total) na espira.
Passo 1
Vamos lá pra mais uma pessoal
O módulo da força eletromotriz induzida em uma espira condutora é igual à taxa de variação com o tempo do fluxo magnético que atravessa a espira. A expressão para calcular a força eletromotriz é a seguinte:
O sinal negativo mostra que a força eletromotriz se opõe à variação do fluxo.
Passo 2
Vamos dizer que o comprimento do lado da espira é . Nesse caso, o fluxo magnético através do circuito é e a fem induzida é:
Como foi dado no enunciado que , a derivada do campo em relação ao tempo é . Substituindo na expressão encontrada acima, temos:
Como o campo magnético aponta para fora do papel e está diminuindo conforme o passar do tempo, a fem induzida tem a mesma polaridade que a fonte, e a fem total é:
Passo 3
O sentido da corrente total nessa espira é anti-horário.
Resposta
- ;
- O sentido da corrente total nessa espira é anti-horário.