Uma barra metálica horizontal , de comprimento e massa , pode escorregar sem atrito sobre dois trilhos verticais condutores, que estão unidos por uma haste horizontal fixa de resistência . As resistências da barra e do trilho são desprezíveis. O conjunto está em uma região onde há um campo magnético constante (uniforme e estacionário, com ).
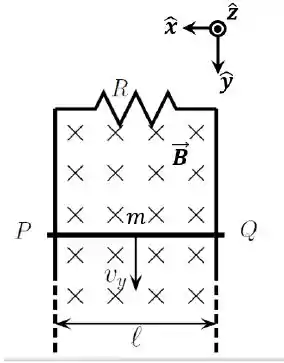
Suponha que, no instante , a barra tenha sido abandonada do repouso e durante seu movimento ela não tenha perdido o contato com os trilhos verticais. Denote por o módulo da aceleração da gravidade ( tem sentido ). Despreze quaisquer efeitos capacitivos ou indutivos no circuito.
Determine o sentido da corrente induzida no circuito.
Calcule a intensidade da corrente induzida no circuito em um instante genérico , em função de , , e . Considere que em a barra ocupava a posição .
Determine a força magnética, , (módulo, direção e sentido) atuando na barra, num instante de tempo , quando a velocidade da mesma tem módulo .
Após algum tempo, a barra entra em movimento uniforme (suponha que esse regime seja atingido antes da barra atingir o solo). Nesse regime, sua velocidade tem módulo (velocidade terminal). Obtenha a expressão para em termos de , , , e .
Passo 1
Determine o sentido da corrente induzida no circuito.
De acordo com a Lei de Lenz, a corrente induzida vai surgir de forma a se opor à variação do fluxo magnético. Vamos lá!
Nesse caso, como o campo magnético é constante, o fluxo magnético através da espira é dado por:
Onde representa a área da mesma.
Conforme a barra cai, a área aumenta e, por consequência, aumenta também o fluxo magnético.
Nesse caso, o campo magnético induzido tentará se opor a esse aumento, estando no sentido oposto do campo magnético externo, logo, no sentido .
Assim, para que o campo magnético induzido tenha esse sentido, é necessário que a corrente induzida, de acordo com a regra da mão direita, esteja no sentido anti-horário.
Passo 2
Calcule a intensidade da corrente induzida no circuito em um instante genérico , em função de , , e . Considere que em a barra ocupava a posição .
Retomando o raciocínio feito no Passo 1, o fluxo magnético através da espira é dado por:
Onde representa a área da espira. Neste caso, como em , , a área da espira será dada por:
De acordo com a Lei de Faraday, a fem induzida será dada por:
Finalmente, a intensidade da corrente induzida será dada por:
Passo 3
Determine a força magnética, , (módulo, direção e sentido) atuando na barra, num instante de tempo , quando a velocidade da mesma tem módulo .
A força magnética sobre um condutor retilíneo é dada por:
Onde é um vetor cujo o módulo é igual ao tamanho da barra, e tem a mesma direção e sentido da corrente. No Passo 1, determinamos que a corrente nesse circuito está no sentido anti-horário, assim, a corrente na barra está no sentido .
Logo:
Além disso:
Dessa forma, teremos:
Passo 4
Após algum tempo, a barra entra em movimento uniforme (suponha que esse regime seja atingido antes da barra atingir o solo). Nesse regime, sua velocidade tem módulo (velocidade terminal). Obtenha a expressão para em termos de , , , e .
Quando a barra entra em movimento uniforme, a força resultante sobre a mesma deve ser nula. Dessa forma, o módulo da força magnética deve ser igual ao peso:
Isolando a velocidade, teremos:
Resposta
Sentido anti-horário.