Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Lenz

Ver Teoria
Exercício 48123456789101112131415161718192021222324252627282930313233343536373839404142434445464749505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697

Enunciado

Ufpe - Física 3 – P3 2018.2 - 2

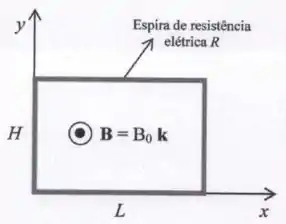
Uma espira condutora retangular, de altura H , largura L e resistência elétrica R está situada no plano x - y como indicado na figura ao lado. A espira está imersa em um campo magnético   B → = B 0 k ^ , onde  k ^ denota o vetor unitário ao longo do eixo z , B 0 = α t 3 y 2 , e α é uma constante positiva.

  1. Calcule o módulo do fluxo magnético através da espira.
  2. Calcule o módulo da corrente induzida na espira. Além disso, determine e justifique o sentido (horário ou anti-horário) da corrente induzida.
  3. Determine o sentido (horário ou anti-horário) do campo elétrico induzido na espira.

Passo 1

a) Antes de começar a fazer as contas, é bom a gente dar uma olhada para a expressão do campo magnético B → primeiro e ver as características que ele tem.

Primeiro, B → depende da posição y , o que significa que ele não é uniforme, ou seja, não tem o mesmo valor em alturas y diferentes. Por outro lado, para um dado instante de tempo t , se fixamos uma altura y qualquer, B → terá o mesmo valor ao longo de todo o comprimento L .

Além de depender do tempo,  B → está sempre saindo do plano da página e é perpendicular a ela. Portanto, o ângulo entre  B → e os elementos  d A → dessa superfície é sempre o mesmo. Vamos escolher, para facilitar nossa vida,  B → paralelo a  d A → , que deixa a expressão para o fluxo magnético da seguinte forma:

Φ B t = ∫ S B → ⋅ d A → = ∫ S B 0 y , t d A   .

Agora, vamos olhar para o elemento de área d A . Para isso, desenhamos na figura abaixo a faixa sombreada indicando esse elemento: d A = L d y .

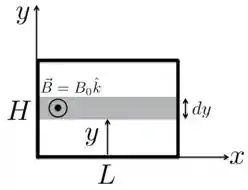
Substituindo d A e B 0 no fluxo, teremos:

Φ B t = α t 3 L ∫ 0 H y 2 d y     ⇒   Φ B t = α t 3 L H 3 3   .

Passo 2

b) Da expressão que acabamos de encontrar para o fluxo magnético, fica claro que Φ B ( t ) aumenta com o tempo, já que o campo magnético aumenta com o tempo para fora da superfície retangular. Por isso, vai aparecer uma fem induzida na espira e, como ela é feita de material condutor, vai ter também uma corrente induzida circulando nela.

Para encontrarmos a fem induzida,

i i n d = ε R = 1 R - d Φ B t d t = α t 2 L H 3 R   .

Como o campo magnético está aumentando com o tempo e está saindo do plano da página, aparece uma fem e também uma corrente induzida que se opõe a essa variação temporal do fluxo. Portanto, i i n d vai circular no sentido horário para que o fluxo do campo magnético induzido que ela produz se oponha à variação temporal de Φ B ( t ) .

Passo 3

c) Como a corrente induzida está no sentido horário, o campo elétrico também estará no sentido horário. De fato, o surgimento desse campo elétrico induzido é que dá origem à corrente induzida.

Resposta

  1. Φ B t = α t 3 L H 3 3   ;
  2. i i n d = ε R = α t 2 L H 3 R   ;
  3. Campo elétrico induzido está no sentido horário.

Exercícios de Livros Relacionados

20- Uma barra metálica com 1.50m de comprimento é puxada para a direita a 5.0m / s regulares e perpendicularmente a um campo magnético uniforme de 0.750T . A barra desliza sobre trilhos metálicos para
17- Use a lei de Lenz para determinar o sentido da corrente induzida que passa no resistor a b indicado na Figura 29.33 , quando ( a ) a chave S é aberta depois de ficar fechada durante alguns minutos
15- Um anel circular está em uma região do espaço onde existe um campo magnético uniforme, como indica a Figura 29.31 . O campo magnético está entrando no plano da figura. Determine o sentido (horário
18- Um tubo de papelão é circundado por dois enrolamentos feitos com dois fios isolados, formando espiras em sentidos contrários, como indica a Figura 29.34 . Os terminais a e b do enrolamento A podem
16- A corrente na Figura 29.32 obedece a equação I t = I 0 e - b t . Em que b0 . Determine o sentido (horário ou anti-horário) da corrente induzida na bobina redonda para t0 .