Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Lenz

Ver Teoria
Exercício 41235678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697

Enunciado

A figura abaixo mostra duas regiões circulares, R 1 e R 2 , de raios r 1 = 20,0   c m e r 2 = 30,0   c m .

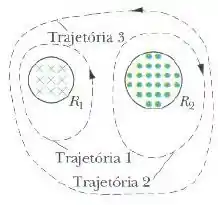
Em R 1 existe um campo magnético uniforme de módulo B 1 = 50,0   m T dirigido para dentro do papel, e em R 2 existe um campo magnético uniforme de módulo B 2 = 75,0   m T dirigido para fora do papel (ignore os efeitos de borda).

Os dois campos estão diminuindo à taxa de 8,50   m T / s . Calcule o valor de ∮ E → ∙ d s → a para a trajetória 1; b para a trajetória 2; c para trajetória 3.

Passo 1

a Calcule o valor de ∮ E → ∙ d s → para a trajetória 1;

De acordo com a Lei de Faraday:

∮ E → ∙ d s → = - ∂ ϕ B ∂ t

Usando a regra da mão direita, vemos que a orientação da trajetória 1 está no sentido contrário ao campo magnético em R 1 , logo:

∮ 1 E → ∙ d s → = ∂ B 1 A 1 ∂ t

∮ 1 E → ∙ d s → = A 1 ∂ B 1 ∂ t

∮ 1 E → ∙ d s → = π r 1 2 ∂ B 1 ∂ t

Onde:

r 1 = 0,2   m

∂ B 1 ∂ t = - 8,5 × 10 - 3   T / s

Logo:

∮ 1 E → ∙ d s → = π 0,2 2 × - 8,5 × 10 - 3

∮ 1 E → ∙ d s → = - 1,07 × 10 - 3 V

Passo 2

b Calcule o valor de ∮ E → ∙ d s → para a trajetória 2;

De acordo com a Lei de Faraday:

∮ E → ∙ d s → = - ∂ ϕ B ∂ t

Usando a regra da mão direita, vemos que a orientação da trajetória 2 está no sentido contrário ao campo magnético em R 2 , logo:

∮ 2 E → ∙ d s → = ∂ B 2 A 2 ∂ t

∮ 2 E → ∙ d s → = A 2 ∂ B 2 ∂ t

∮ 2 E → ∙ d s → = π r 2 2 ∂ B 2 ∂ t

Onde:

r 2 = 0,3   m

∂ B 2 ∂ t = - 8,5 × 10 - 3   T / s

Logo:

∮ 2 E → ∙ d s → = π 0,3 2 × - 8,5 × 10 - 3

∮ 2 E → ∙ d s → = - 2,40 × 10 - 3 V

Passo 3

c Calcule o valor de ∮ E → ∙ d s → para a trajetória 3;

Vemos que a trajetória 3 tem a mesma orientação da trajetória 1 e orientação contrária à trajetória 2. Portanto:

∮ 3 E → ∙ d s → = ∮ 1 E → ∙ d s → - ∮ 2 E → ∙ d s →

∮ 3 E → ∙ d s → = - 1,07 × 10 - 3 - - 2,40 × 10 - 3

∮ 3 E → ∙ d s → = 1,33 × 10 - 3 V

Resposta

a

∮ 1 E → ∙ d s → = - 1,07 × 10 - 3 V

b

∮ 2 E → ∙ d s → = - 2,40 × 10 - 3 V

c

∮ 3 E → ∙ d s → = 1,33 × 10 - 3 V

Exercícios de Livros Relacionados

20- Uma barra metálica com 1.50m de comprimento é puxada para a direita a 5.0m / s regulares e perpendicularmente a um campo magnético uniforme de 0.750T . A barra desliza sobre trilhos metálicos para
17- Use a lei de Lenz para determinar o sentido da corrente induzida que passa no resistor a b indicado na Figura 29.33 , quando ( a ) a chave S é aberta depois de ficar fechada durante alguns minutos
15- Um anel circular está em uma região do espaço onde existe um campo magnético uniforme, como indica a Figura 29.31 . O campo magnético está entrando no plano da figura. Determine o sentido (horário
18- Um tubo de papelão é circundado por dois enrolamentos feitos com dois fios isolados, formando espiras em sentidos contrários, como indica a Figura 29.34 . Os terminais a e b do enrolamento A podem
16- A corrente na Figura 29.32 obedece a equação I t = I 0 e - b t . Em que b0 . Determine o sentido (horário ou anti-horário) da corrente induzida na bobina redonda para t0 .