4 – O campo elétrico de uma onda eletromagnética plana se propaga no vácuo é dado por .
a) Determine o vetor campo magnético desta onda.
b) Determine o vetor de Poynting desta onda.
c) Considerando que a onda incide normalmente sobre um disco perfeitamente absorvedor de raio , calcule a energia transferida ao disco durante um intervalo de tempo correspondente a periodos. Expresse sua resposta em termos das grandezas dadas acima.
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nessa questão temos apenas uma onda eletromagnética que se propaga no vácuo e seu campo elétrico é descrito pela equação .
Com essas informações temos que obter algumas respostas sobre essa onda.
Primeiro, no item a), temos que determinar o vetor campo magnético da onda.
Segundo, no item b), temos que obter o vetor de Poynting da onda.
E por último, no item c), temos que obter a energia transferida para um disco perfeitamente absorvente de raio em um intervalo de tempo de dois períodos da onda.
Parece simples? Como podemos fazer isso? 🤔🤔
Na primeira pergunta vamos usar a propriedade de propagação da onda que diz que a velocidade da onda eletromagnética é igual a razão entre o valor absoluto do campo elétrico e o valor absoluto do campo magnético.
Na segunda pergunta vamos obter o vetor de Poynting usando sua relação com o vetor campo elétrico e o vetor campo magnético.
E na terceira pergunta vamos usar a ideia de intensidade de radiação para obter a resposta.
Preparado? 🤩
Passo 2
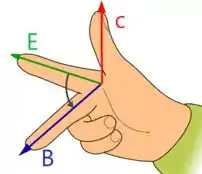
Para determinar o campo magnético da onda, temos que ter em mente uma propriedade que diz que a direção de propagação da onda, o seu campo elétrico e seu campo magnético seguem a regra da mão direita.
Uma equação muito interessante diz que
Logo, vemos que
Como o campo elétrico propaga na direção , o campo magnético deve propagar na direção já que pela equação propaga em positivo.
Então se , temos
Entendeu essa parte? 😎
Passo 3
Na segunda pergunta, vamos obter o vetor de Poynting através da sua formulinha
Calculando o produto vetorial entre e , de forma matricial, temos
Como , vamos obter
Substituindo em
Assim encontramos o vetor de Poynting e veja que ele deve apontar no sentido de propagação da onda!
Interessante, não é? 😁
Passo 4
Por último, vamos encontrar a energia absorvida pelo disco através da intensidade da onda.
Onde é a intensidade, é a energia da onda, é a área de absorção e é o intervalo de tempo.
Podemos calcular a intensidade como
Igualando as duas equações, temos
Isolando a energia da onda
Mas espera aí! O que é e dado que nosso objeto absorvente é um disco de raio e é exposto num intervalo de tempo de dois períodos de onda.
A área superior de um disco é o mesmo que a área do círculo, ou seja
Está acompanhando? 😉
Passo 5
Resta apenas encontrar , se o disco é exposto em um intervalo de dois períodos de onda, temos
Lembra que o período de uma onda é dada pelo comprimento de onda dividido pela velocidade da onda ?
O comprimento de onda, por sua vez, é dado por e a velocidade da onda eletromagnética é dada por
Fazendo essas substituições em , vamos obter
Substituindo em ...
Agora sim! Substituindo e em , temos
Simplificando...
Expressão estranha, não é?
Mas a energia que o disco absorve da onda é isso aí, acredita? 👀
Fim! Iae, o que achou? Responde Aí! 😁

Resposta
A)
B)
C)