Uma onda eletromagnética plana monocromática, com polarização linear e com frequência , se propaga no vácuo tal que seu vetor de Poynting está no sentido e tem amplitude máxima igual a na origem, para .
a) Escreve a expressão para o vetor de Poynting, em função do tempo e do espaço.
b) Sabendo que a polarização está no eixo e que o campo elétrico é positivo na origem para , escreva a expressão para o campo magnético, em função do tempo e do espaço.
c) A lei de Ampère, em sua formulação original, está dada por ou (em sua forma diferencial). Mostre que, escrita desta maneira, a Lei de Ampère não contempla situações fora da magnetostática (densidades de corrente variáveis).
d) A partir da Lei de Gauss na forma integral, chegue à sua formulação da forma diferencial.
Passo 1
Fala pessoal, prontos para uma questão de física 4?
Nesse problema vamos discutir sobre campos eletromagnéticos que se propagam como ondas eletromagnéticas!
No item (a) temos que dar uma expressão para o vetor de Poyting. No geral, esse vetor é dado por
O vetor de Poynting é o produto vetorial do campo elétrico pelo campo magnético. Esse vetor tem algumas propriedades importantes, vou destacar uma delas: ele aponta na direção de propagação da onda, sendo perpendicular tanto a como a .
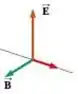
Observando a figura, o vetor de Poynting é representado em vermelho!
Sabemos que numa onda plana, os campos elétricos e magnéticos que se propagam na direção terão seus módulos dados por
Vale lembrar ainda que existe a relação . Não representei as direções dos campos elétrico e magnéticos pois não podemos saber isso à priori pelos dados do enunciado do item (a). O ponto importante é o seguinte: como o vetor de Poynting é o produto vetorial desses dois vetores, seu módulo será dado por
Podemos escrever ainda
Falta a gente achar e !
Passo 2
Para achar e , temos que olhar para a condição: “tem amplitude máxima igual a na origem, para ”.
Com isso, achamos que e para e (origem), devemos ter
Isso deve acontecer para que a amplitude seja máxima! Com isso, temos que
Portanto, podemos tomar :
Achar o número de onda e a frequência angular é tranquilo:
Como , temos
Assim,
Logo,
Para terminar o problema, basta colocar o versor para dar a resposta vetorialmente:
Passo 3
Agora vamos para o item (b)!
Ele disse que a polarização está na direção : isso significa que o campo elétrico está na direção ! Portanto, podemos escrever
Note que já não escrevi a constante de fase pois vimos no item (a) que .
O problema quer saber qual o vetor do campo magnético. Nós sabemos que está na direção e na direção :
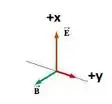
Desta forma, o campo deve estar na direção para que tudo seja consistente! Note que na figura, a direção é oposta ao campo . Com isso, podemos escrever:
Passo 4
No passo 1, vimos que a amplitude do vetor de Poynting era
Logo,
Substituindo , e :
Assim,
Portanto,
Aqui nessa última passagem substitui e que achamos no item (a).
Passo 5
Partiu item (c)!!!
Esse item é bem teórico, inclusive valia ponto bônus na questão, então não precisa se preocupar se você não souber muito bem essa parte...
O enunciado fala sobre a lei de Ampère na forma diferencial:
Ele quer que a gente mostre que essa lei, escrita dessa forma, não vale fora da magnetostática. Mas o que diabos é magnetostática?
A magnetostática cuida de problemas em que as correntes e os campos magnéticos são estáticos, ou seja, não varia no tempo. Nessa situação, a lei de Ampére escrita do jeitinho que eu escrevi é perfeita. Todavia, se as correntes variarem com o tempo, devemos adicionar um termo extra na equação: foi isso que Maxwell fez e por isso ele é tão famoso! Mas não vou entrar em muito detalhe aqui, vou fazer só o que o exercício pediu...
O exercício pediu para mostra que a Lei de Ampère não contempla situações fora da magnetostática e é isso que vamos fazer!
Para resolver esse problema, vamos olhar para a equação da continuidade:
Com isso, tiramos que
Note que se tivermos na magnetostática, a derivada de no tempo se anula, de modo que achamos . Mas fora da magnetostática isso não acontece!
Agora vamos voltar para a Lei de Ampère e tomar o divergente em ambos os lados:
Com isso, temos:
Aqui vem o pulo do gato: o divergente de um rotacional de qualquer vetor é sempre nulo, de modo que o lado esquerdo da equação é zero:
Acontece que fora da magnetostática o lado direito não é zero pois . Aqui aparece o problema! Era isso que o problema queria que você fizesse...
Eu sei que é difícil, é um conteúdo totalmente teórico e não trivial, mas que eu particularmente acho bem bonitinho 😊.
Passo 6
Assim como o item (c), o item (d) também era um bônus...
O exercício quer que a gente deduza a lei de Gauss na forma diferencial () a partir de sua forma integral:
Para fazer isso, usamos o teorema de Gauss (ou do divergente) que você deve ter aprendido em cálculo vetorial:
O teorema diz que a integral de superfície (fluxo) de um vetor em uma superfície fechada é igual a integral de volume do divergente desse vetor.
Além disso, a carga pode ser escrita como a integral de volume da densidade de carga:
Substituindo isso na lei de Gauss:
Jogando tudo para o mesmo lado temos
Para que isso seja verdade, o integrando deve ser nulo, de modo que
Ou ainda,
Era isso que o exercício queria que você fizesse! 😉
Resposta
Demonstração.