Uma onda plana eletromagnética linearmente polarizada, propagando-se no vácuo no sentido positivo do eixo z, tem comprimento de onda e intensidade .
(a)Se a direção de polarização da onda faz 45° com o eixo y, determine a expressão do campo elétrico em função do tempo e do espaço (a menos de uma fase constante).
Passo 1
Para determinarmos o valor do campo elétrico precisamos antes de tudo nos lembrar de como escrevemos ele, para isso devemos nos lembrar da fórmula
Mas temos que tomar um cuidado, o coeficiente K sempre multiplica a variável que está na direção da propagação da nossa onda, e no enunciado foi dito que essa direção é a Z, logo teremos que
Passo 2
Outra coisa que precisamos determinar na nossa equação é o valor de , para isso temos que analisar os valores dados no enunciado.
É dito que a nossa onda polarizada tem o seguinte aspecto
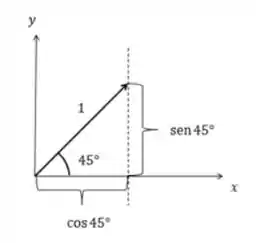
Dessa forma podemos escrever o nosso vetor unitário em função de x e y da seguinte maneira
Como tanto o valor de teremos que
Agora só precisamos determinar o valor de , e
Passo 3
Agora temos que saber que o nosso número de onda K pode ser determinado através da fórmula
e que a nossa frequência angular pode ser definida pela fórmula
Sabemos pelo enunciado e pelo formulário que
Calculando primeiro o fator de onda teremos que
Calculando agora o valor da frequência angula teremos que
Calculando isso, falta apenas o valor de , mas como faremos para calcular esse valor?
Passo 4
Aqui termos que lembrar de uma fórmula muito importante que relaciona a amplitude do nosso campo elétrico e a intensidade da onda que foi dada no nosso enunciado, e essa fórmula é exatamente
Isolando teremos que
Sabemos que
Isolando teremos que
Substituindo na equação teremos que
Sabemos que
Substituindo
Logo teremos que
Passo 5
Agora que temos todas as fórmulas basta que substituamos tudo na fórmula inicial, assim teremos que